Точки A,B,C лежат на одной прямой ,а точка O не лежит на этой прямой .Будут ли треугольники AOB и BOC с основаниями AB,BC равнобедренными? Обоснуйте ответ
Даны координаты пирамиды: A1(6,8,2), A2(5,4,7), A3(2,4,7), A4(7,3,7). 1) Координаты векторов. Координаты векторов находим по формуле: X = xj - xi; Y = yj - yi; Z = zj - zi здесь X,Y,Z координаты вектора; xi, yi, zi - координаты точки Аi; xj, yj, zj - координаты точки Аj; Например, для вектора A1A2 X = x2 - x1; Y = y2 - y1; Z = z2 - z1 X = 5-6; Y = 4-8; Z = 7-2 A1A2(-1;-4;5) A1A3(-4;-4;5) A1A4(1;-5;5) A2A3(-3;0;0) A2A4(2;-1;0) A3A4(5;-1;0)
2) Модули векторов (длина ребер пирамиды) Длина вектора a(X;Y;Z) выражается через его координаты формулой: a = √(X² + Y² + Z²). Нахождение длин ребер и координат векторов. Вектор А1A2={xB-xA, yB-yA, zB-zA} -1 -4 5 L = 6,480740698. Вектор A2A3={xC-xB, yC-yB, zC-zB} -3 0 0 L =3. Вектор А1A3={xC-xA, yC-yA, zC-zA} -4 -4 5 L = 7,549834435. Вектор А1A4={xD-xA, yD-yA, zD-zA} 1 -5 5 L =7,141428429. Вектор A2A4={xD-xB, yD-yB, zD-zB} 2 -1 0 L = 2,236067977. Вектор A3A4={xD-xC, yD-yC, zD-zC} 5 -1 0 L = 5,099019514.
3) Уравнение прямой Прямая, проходящая через точки A1(x1; y1; z1) и A2(x2; y2; z2), представляется уравнениями: Параметрическое уравнение прямой: x=x₀+lt y=y₀+mt z=z₀+nt Уравнение прямой A1A2(-1,-4,5) Параметрическое уравнение прямой: x=6-t y=8-4t z=2+5t.
5) Уравнение прямой А4М, перпендикулярной к плоскости А1А2А3, - это высота из точки А4 на основание пирамиды. Прямая, проходящая через точку M₀(x₀;y₀;z₀) и перпендикулярная плоскости Ax + By + Cz + D = 0 имеет направляющий вектор (A;B;C). Уравнение плоскости A1A2A3: - 5y - 4z + 48 = 0. Уравнение А4М:
7) Уравнение прямой А3N, параллельной прямой А1А2.
Необходимая для решения точка А3(2; 4; 7) задана по условию, а направляющий вектор для искомой прямой возьмём тот же, что для прямой А1А2, так как они параллельны: n=(-1;-4;5).
Здесь даже чертеж не нужен (хотя он для наглядности приложен)
Помним теорему синусов треугольника:
Где угол лежит напротив стороны , угол лежит напротив стороны , а угол лежит напротив стороны , а - радиус описанной около треугольника окружности (правда, окружность в этой задаче нам не нужна)
Учитывая, что
Но тогда теорему синусов можно переписать так:
Что и требовалось доказать.
Можно ещё по-другому пойти.
Смотрим на рисунок. (нижние углы), то есть треугольник равнобедренный с основанием , значит, боковые стороны равны, то есть
Далее, , то треугольник равнобедренный с основанием , боковые стороны равны, то есть
1) Координаты векторов.
Координаты векторов находим по формуле:
X = xj - xi; Y = yj - yi; Z = zj - zi
здесь X,Y,Z координаты вектора; xi, yi, zi - координаты точки Аi; xj, yj, zj - координаты точки Аj;
Например, для вектора A1A2
X = x2 - x1; Y = y2 - y1; Z = z2 - z1
X = 5-6; Y = 4-8; Z = 7-2
A1A2(-1;-4;5)
A1A3(-4;-4;5)
A1A4(1;-5;5)
A2A3(-3;0;0)
A2A4(2;-1;0)
A3A4(5;-1;0)
2) Модули векторов (длина ребер пирамиды)
Длина вектора a(X;Y;Z) выражается через его координаты формулой:
a = √(X² + Y² + Z²).
Нахождение длин ребер и координат векторов.
Вектор А1A2={xB-xA, yB-yA, zB-zA} -1 -4 5 L = 6,480740698.
Вектор A2A3={xC-xB, yC-yB, zC-zB} -3 0 0 L =3.
Вектор А1A3={xC-xA, yC-yA, zC-zA} -4 -4 5 L = 7,549834435.
Вектор А1A4={xD-xA, yD-yA, zD-zA} 1 -5 5 L =7,141428429.
Вектор A2A4={xD-xB, yD-yB, zD-zB} 2 -1 0 L = 2,236067977.
Вектор A3A4={xD-xC, yD-yC, zD-zC} 5 -1 0 L = 5,099019514.
3) Уравнение прямой
Прямая, проходящая через точки A1(x1; y1; z1) и A2(x2; y2; z2), представляется уравнениями:
Параметрическое уравнение прямой:
x=x₀+lt
y=y₀+mt
z=z₀+nt
Уравнение прямой A1A2(-1,-4,5)
Параметрическое уравнение прямой:
x=6-t
y=8-4t
z=2+5t.
4) Уравнение плоскости А1А2А3.
x-6 y-8 z-2
-1 -4 5-4 -4 5 = 0
(x-6)((-4)*5-(-4)*5) - (y-8)((-1)*5-(-4)*5) + (z-2)((-1)*(-4)-(-4)*(-4)) =
= - 15y - 12z + 144 = 0
Упростим выражение: - 5y - 4z + 48 = 0.
5) Уравнение прямой А4М, перпендикулярной к плоскости А1А2А3, - это высота из точки А4 на основание пирамиды.
Прямая, проходящая через точку M₀(x₀;y₀;z₀) и перпендикулярная плоскости Ax + By + Cz + D = 0 имеет направляющий вектор (A;B;C).
Уравнение плоскости A1A2A3: - 5y - 4z + 48 = 0.
Уравнение А4М:
6) Уравнение плоскости, проходящей через точку перпендикулярно вектору A1A2.
Уравнение плоскости, проходящей через точку M₀(x₀, y₀, z₀) перпендикулярно вектору N = (l,m,n), имеет вид:
l(x- x₀) + m(y- y₀) + n(z- z₀) = 0
Координаты точки A4(7;3;7)
Координаты вектора A1A2(-1;-4;5)
-1(x - 7) + (-4)(y - 3) + 5(z - 7) = 0
Искомое уравнение плоскости:
-x - 4y + 5z-16 = 0.
7) Уравнение прямой А3N, параллельной прямой А1А2.
Необходимая для решения точка А3(2; 4; 7) задана по условию, а направляющий вектор для искомой прямой возьмём тот же, что для прямой А1А2, так как они параллельны: n=(-1;-4;5).
ответ: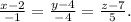
Здесь даже чертеж не нужен (хотя он для наглядности приложен)
Помним теорему синусов треугольника:
Где угол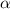 лежит напротив стороны
лежит напротив стороны  , угол
, угол 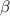 лежит напротив стороны
лежит напротив стороны 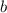 , а угол
, а угол 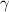 лежит напротив стороны
лежит напротив стороны  , а
, а 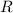 - радиус описанной около треугольника окружности (правда, окружность в этой задаче нам не нужна)
- радиус описанной около треугольника окружности (правда, окружность в этой задаче нам не нужна)
Учитывая, что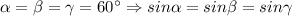
Но тогда теорему синусов можно переписать так:
Что и требовалось доказать.
Можно ещё по-другому пойти.
Смотрим на рисунок.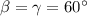 (нижние углы), то есть треугольник равнобедренный с основанием
(нижние углы), то есть треугольник равнобедренный с основанием  , значит, боковые стороны равны, то есть
, значит, боковые стороны равны, то есть 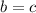
Далее,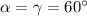 , то треугольник равнобедренный с основанием
, то треугольник равнобедренный с основанием 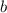 , боковые стороны равны, то есть
, боковые стороны равны, то есть 
Ну и завершающий вывод:
Что и требовалось доказать.