11.
Дано:
ΔАВС - равнобедренный
АС = ВС = 13
АВ = 10
Найти:
АС - высоту. опущенную на боковую сторону
СD - высота равнобедренного треугольника. опущенная на основание, является и медианой. Поэтому AD = BD = 0.5AB = 0.5 · 10 = 5.
По теореме Пифагора
АС² = CD² + AD²
13² = CD² + 5²
CD² = 13² - 5² = 144 = 12²
CD = 12
Площадь треугольника АВС
S = 0.5 CD · AB = 0.5 · 12 · 10 = 60
Площадь треугольника АВС можно также вычислить и так:
S = 0.5 BC · AE
откуда
АЕ = 2S : BC = 2 · 60 : 13 = 9 ≈ 9.23
АЕ = 9 ≈ 9.23
12.
MKNR - ромб
KR = 10 - 1-я диагональ ромба
MN = 12 - 2-я диагональ ромба
МК - сторону ромба
Пусть О - точка пересечения диагоналей ромба.
Диагонали ромба делятся точкой пересечения пополам, поэтому
КО = 0,5 KR = 0.5 · 10 = 5
МО = 0,5 MN = 0.5 · 12 = 6
Диагонали ромба пересекаются под прямым углом, поэтому
КО ⊥ МО и ΔМКО - прямоугольный с гипотенузой МК.
МК² = КО² + МО²
МК² = 5² + 6² = 61
МК = √61 ≈ 7,81
Сторона ромба МК =√61 ≈ 7,81
1. Два суміжні кути мають спільну вершину і одну спільну сторону, дві інші (не спільні) сторони утворюють пряму лінію.
2. Згідно з теореми: ∠COK=∠MOD=1100 як вертикальні кути.
Градусна міра кута дорівнює сумі градусних мір кутів, на які він розбивається будь-яким променем, що проходить між його сторонами.
3.Якщо два суміжні кути рівні, то вони прямі.
4.Бісектриси суміжних кутів утворюють прямий кут
5. Разом 180°
6. два кути називаються вертикальними якщо вони утворені перетином двох прямих і не є прилеглими.
7. Ні
8. Кут між прямими, що перетинаються, не перевищує 90°
11.
Дано:
ΔАВС - равнобедренный
АС = ВС = 13
АВ = 10
Найти:
АС - высоту. опущенную на боковую сторону
СD - высота равнобедренного треугольника. опущенная на основание, является и медианой. Поэтому AD = BD = 0.5AB = 0.5 · 10 = 5.
По теореме Пифагора
АС² = CD² + AD²
13² = CD² + 5²
CD² = 13² - 5² = 144 = 12²
CD = 12
Площадь треугольника АВС
S = 0.5 CD · AB = 0.5 · 12 · 10 = 60
Площадь треугольника АВС можно также вычислить и так:
S = 0.5 BC · AE
откуда
АЕ = 2S : BC = 2 · 60 : 13 = 9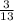 ≈ 9.23
≈ 9.23
АЕ = 9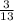 ≈ 9.23
≈ 9.23
12.
Дано:
MKNR - ромб
KR = 10 - 1-я диагональ ромба
MN = 12 - 2-я диагональ ромба
Найти:
МК - сторону ромба
Пусть О - точка пересечения диагоналей ромба.
Диагонали ромба делятся точкой пересечения пополам, поэтому
КО = 0,5 KR = 0.5 · 10 = 5
МО = 0,5 MN = 0.5 · 12 = 6
Диагонали ромба пересекаются под прямым углом, поэтому
КО ⊥ МО и ΔМКО - прямоугольный с гипотенузой МК.
По теореме Пифагора
МК² = КО² + МО²
МК² = 5² + 6² = 61
МК = √61 ≈ 7,81
Сторона ромба МК =√61 ≈ 7,81
1. Два суміжні кути мають спільну вершину і одну спільну сторону, дві інші (не спільні) сторони утворюють пряму лінію.
2. Згідно з теореми: ∠COK=∠MOD=1100 як вертикальні кути.
Градусна міра кута дорівнює сумі градусних мір кутів, на які він розбивається будь-яким променем, що проходить між його сторонами.
3.Якщо два суміжні кути рівні, то вони прямі.
4.Бісектриси суміжних кутів утворюють прямий кут
5. Разом 180°
6. два кути називаються вертикальними якщо вони утворені перетином двох прямих і не є прилеглими.
7. Ні
8. Кут між прямими, що перетинаються, не перевищує 90°