Точки A, М и О лежат на прямой a, перпендикулярной к плоскости α, а точки О, B, С и D лежат в плоскости α. Какие из следующих углов являются прямыми: АОВ, МОС, DAM, DOA, BMO? Подсказка
Прямая a ⊥ , поэтому прямая a перпендикулярна к любой прямой лежащей в плоскости . Чтобы прямая плоскости α, необходимо, чтобы точки прямой принадлежали плоскости α.

BO ⊂ , ∠AOB = 90°;

⊂ α, ∠AOC = 90°;

DO ⊂ α, ∠ = 90°;

DA ⊄ α, ∠DAM ≠ 90°;

⊄ α, ∠BMO ≠ 90°.

ответ: .

Варианты ответа:

∠AOB, ∠AOC, ∠DOA - 1

DOA - 2

α - 3

BM - 4

OC - 5

принадлежала - 6

ответ: 2

Объяснение:

, где

Sп.п - площадь полной поверхности

Sосн. - площадь основания

Sбок - площадь боковой грани

Рассмотрим основание призмы

Мы можем узнать сторону основания(понадобиться позже). Тк. по свойству ромба его диагонали перпендикулярны и делятся пополам, то ромб разбит на 4 равных прямоугольных треугольника с катетами 5 и 12. Рассмотрим 1 из них.

По т. Пифагора:

Площадь ромба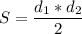

Подставляем в формулу площади полной поверхности призмы

Мы знаем, что боковая грань - прямоугольник,т.е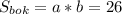  

Т.к. нам известна одна из сторон(сторона основания, которая равна 13), то мы можем найти и боковое ребро

Объяснение:

Строим сторону АВ = 14 м, взяв для простоты 1 мм за 1 м. С вершинами в точках А и В, со стороной АВ строим углы в 120°. Откладываем на полученных сторонах отрезки АС = BD = 14 м и строим с вершинами в точках С и D углы 120°. Откладываем на полученных сторонах СМ = DP = 14 м, соединяем точки М и Р. Шестиугольник ABDPMC есть план Семиглавой башни. Этот многоугольник называется правильным, так как у него стороны и углы равны. Точка О есть центр правильного многоугольника. Из него сторона АВ видна под углом AOB.