Точки А1, В1 и C1 — середины сторон BC, CA и AB треугольника АВС. Известно, что
A = 44°, B = 54°. Найдите сумму C1 A1 C + A, B1 A+B1 C1 B.

ток норм ответ ко павильно ответит подпишусь и постараюсь поставить лайки на все ааши ответы​

Для любой правильной призмы справедливы формулы:

Площадь боковой поверхности:

Sбок = Pосн · h, где

Росн - периметр основания,

h - высота.

Площадь полной поверхности:

Sполн = Sбок + 2Sосн

Объем:

V = Sосн · h

____________________

a - сторона основания.

____________________

Правильная треугольная призма:

в основании лежит правильный треугольник, значит

Sосн =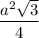

Sбок = 3а · h

Sполн = 3a · h + 2 · a²√3/4 = 3ah + a²√3/2

____________________

Правильная четырехугольная призма:

в основании - квадрат, значит

Sосн = a²

Sбок = 4ah

Sполн = 4ah + 2a²

V = a²h

____________________

Правильная шестиугольная призма:

Sосн =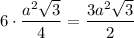

Sбок = 6ah

Sполн = 6ah + 2 · 3a²√3/2 = 6ah + 3a²√3

1) Центром вписанной окружности треугольника является точка пересечения биссектрис.

Биссектриса к основанию равнобедренного треугольника является высотой и медианой.

MO - биссектриса, KE - биссектриса, высота и медиана.

ME=EN=10

По теореме Пифагора

KE =√(MK^2-ME^2) =12*2 =24

По теореме о биссектрисе

KO/OE =MK/ME =13/5 => OE =5/18 KE =20/3  

Или по формулам

S=pr

S=√[p(p-a)(p-b)(p-c)], где p=(a+b+c)/2

Отсюда

r=√[(p-a)(p-b)(p-c))/p]

при a=b

r=c/2 *√[(a -c/2)/(a +c/2)] =10*√(16/36] =20/3

3) Вписанный угол, опирающийся на диаметр - прямой, K=90

MN =2*OM =26

По теореме Пифагора

KN =√(MN^2-MK^2) =5*2 =10

P(KMN) =2(5+12+13) =60