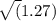Решение. Проведем отрезки BD и CE. Пусть они пересекаются в точке О. Заметим, что треугольники BCD и CDE равнобедренные с углом 108 при вершине, а значит, углы при основании равны 36 (они отмечены на рисунке одной дугой). Тогда BCE = BDE = 72. Угол COD равен 108 (т.к. в треугольнике COD два угла по 36). Поэтому COB = 180108 = 72. Углы по 72 отмечены на рисунке двумя дугами. Получаем, что треугольники CBO и DEO равнобедренные. Значит, AB = BO =BC = CD = DE = EO = х. Заметим, что OBA = 9636 = 60. Значит, треугольник OBA равнобедренный с углом 60 при вершине, т.е. равносторонний. Поэтому AO = x. Вычислим угол AOE AOE = EOBAOB = 10860 = 48. Треугольник AOE равнобедренный с углом 48 при вершине. Поэтому OEA = (18048)/2 = 66. Получаем, что угол E пятиугольника равен AED = AEO+OED = 66+36 = 10
Надеюсь корни вы уже учили, так как целого числа тут не получится. Эта задача очень проста, так как центры окружностей совпадают. Первым действием обозначим радиус меньшей окружности за r(в дальнейшем будем называть эту окружность первой (т.е.1)) , тогда радиус большей окружности ( окружности 2) будет равен 2*r. По формуле площади окружности получаем S1(площадь первой окружности)=пи*r*r, где пи- константа и равно 3,14, а S2(Площадь окружности 2)=пи*(2r)*(2r)=пи*4*r*r.В свою очередь площадь нашего кольца будет равна S2-S1=пи*(4*r*r-r*r)=пи*3*r*r, мы получаем уравнение 3,14*3*r*r=12, которое совсем не сложно решить, осуда получаем,что пи примерно равно
ответ. 102.
Объяснение:
Решение. Проведем отрезки BD и CE. Пусть они пересекаются в точке О. Заметим, что треугольники BCD и CDE равнобедренные с углом 108 при вершине, а значит, углы при основании равны 36 (они отмечены на рисунке одной дугой). Тогда BCE = BDE = 72. Угол COD равен 108 (т.к. в треугольнике COD два угла по 36). Поэтому COB = 180108 = 72. Углы по 72 отмечены на рисунке двумя дугами. Получаем, что треугольники CBO и DEO равнобедренные. Значит, AB = BO =BC = CD = DE = EO = х. Заметим, что OBA = 9636 = 60. Значит, треугольник OBA равнобедренный с углом 60 при вершине, т.е. равносторонний. Поэтому AO = x. Вычислим угол AOE AOE = EOBAOB = 10860 = 48. Треугольник AOE равнобедренный с углом 48 при вершине. Поэтому OEA = (18048)/2 = 66. Получаем, что угол E пятиугольника равен AED = AEO+OED = 66+36 = 10
Надеюсь корни вы уже учили, так как целого числа тут не получится. Эта задача очень проста, так как центры окружностей совпадают. Первым действием обозначим радиус меньшей окружности за r(в дальнейшем будем называть эту окружность первой (т.е.1)) , тогда радиус большей окружности ( окружности 2) будет равен 2*r. По формуле площади окружности получаем S1(площадь первой окружности)=пи*r*r, где пи- константа и равно 3,14, а S2(Площадь окружности 2)=пи*(2r)*(2r)=пи*4*r*r.В свою очередь площадь нашего кольца будет равна S2-S1=пи*(4*r*r-r*r)=пи*3*r*r, мы получаем уравнение 3,14*3*r*r=12, которое совсем не сложно решить, осуда получаем,что пи примерно равно