Объяснение: обозначим вершины треугольника А В С, пропорции 3: 5 : 7 как АВ=3х, ВС=5х, АС=7х и зная, что периметр треугольника составляет 60см составим уравнение:
3х+5х+7х=60
15х=60
х=60÷15
х=4
Теперь найжем каждую сторону треугольника:
1) АВ=3х=3×4=12см
2)ВС= 5х=5×4=20см
3) АС=7х=7×4=28см
Так как треугольник DEF вписан в ∆АВС с середин сторон, то по правилам средней линии треугольника, средняя линия параллельная одной из его сторон равна половине этой стороны.
Поэтому EF || АВ и EF=×AB =12÷2=6 см
DF || BC и EF=×BC=20÷2=10см
DE || AC; DE=×AC=28÷2=14см
тогда периметр второго треугольника составит: Р=6+10+14=30см
треугольнике ABC со сторонами AB=2 см, BC=3 см и AC=3 см проведена биссектриса BM. Найдите длины отрезков AM и MC.
№2 В треугольнике MNKизвестны длины сторон MN=4 см,NK=5 см, NP — биссектриса, а разность длин отрезковMP и PKравна 0,5 см. Найдите MPи PK.
№3 треугольнике DEP проведена биссектрисаEK. Найдите стороныDE и EP,если DK=3 см, KP=4 см, а периметр треугольника DEP равен 21 см.
№4 В треугольнике ABC: BC-AB=3 см, биссектриса BD делит сторону AC на отрезки AD=2 см и DC=3 см. Найдите длины сторон AB и BC
№6 Периметр треугольника CDE равен 55 см. В этот треугольник вписан ромб DMFN так, что вершиныM,F и N лежат соответственно на сторонах CD,CE и DE. Найдите стороны CB и DE, если CF=8 см;EF=12 см. В прямоугольном треугольнике проведена биссектриса острого угла. Известно что эта биссектриса делит противолежащий катет на отрезки 4 см и 5 см. Найдите площадь прямоугольного треугольника.
Точка O на гипотенузе равноудалена от двух катетов прямоугольного треугольника и делит
ответ: 1 сторона=6см
2сторона=10см
3 сторона 14см
Р=30см
Объяснение: обозначим вершины треугольника А В С, пропорции 3: 5 : 7 как АВ=3х, ВС=5х, АС=7х и зная, что периметр треугольника составляет 60см составим уравнение:
3х+5х+7х=60
15х=60
х=60÷15
х=4
Теперь найжем каждую сторону треугольника:
1) АВ=3х=3×4=12см
2)ВС= 5х=5×4=20см
3) АС=7х=7×4=28см
Так как треугольник DEF вписан в ∆АВС с середин сторон, то по правилам средней линии треугольника, средняя линия параллельная одной из его сторон равна половине этой стороны.
Поэтому EF || АВ и EF=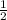
×AB =12÷2=6 см
DF || BC и EF=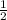
×BC=20÷2=10см
DE || AC; DE=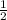
×AC=28÷2=14см
тогда периметр второго треугольника составит: Р=6+10+14=30см
треугольнике ABC со сторонами AB=2 см, BC=3 см и AC=3 см проведена биссектриса BM. Найдите длины отрезков AM и MC.
№2 В треугольнике MNKизвестны длины сторон MN=4 см,NK=5 см, NP — биссектриса, а разность длин отрезковMP и PKравна 0,5 см. Найдите MPи PK.
№3 треугольнике DEP проведена биссектрисаEK. Найдите стороныDE и EP,если DK=3 см, KP=4 см, а периметр треугольника DEP равен 21 см.
№4 В треугольнике ABC: BC-AB=3 см, биссектриса BD делит сторону AC на отрезки AD=2 см и DC=3 см. Найдите длины сторон AB и BC
№6 Периметр треугольника CDE равен 55 см. В этот треугольник вписан ромб DMFN так, что вершиныM,F и N лежат соответственно на сторонах CD,CE и DE. Найдите стороны CB и DE, если CF=8 см;EF=12 см. В прямоугольном треугольнике проведена биссектриса острого угла. Известно что эта биссектриса делит противолежащий катет на отрезки 4 см и 5 см. Найдите площадь прямоугольного треугольника.
Точка O на гипотенузе равноудалена от двух катетов прямоугольного треугольника и делит