Смотрите. Берем треугольник АВС, а рядом с ним рисуем (или воображаем, что проще) треугольник МВР. АВ/МВ=3. Коэффициент подобия 3. Важно помнить, что, если коэффициент подобия больше единицы, то знаичит первый треугольник больше второго. Площадь АВС в 3 в квадрате, то есть в 9 раз больше, чем площадь МВР.
Теперь берем треугольник МВР, а рядом рисуем АВС. МВ/АВ=1/3. Коэффициент подобия 1/3. Это значит, что первый треугольник меньше второго. Площадь МВР составляет 1/3 в квадрате или 1/9 часть площади АВС. Вот и все премудрости. Просто здесь важно стороны какого треугольника являются делимым, а какие делителем. Ведь в операции деления, в отличие от операции умножения, важен порядок. А, находя коэффициенты подобия, мы именно делим!
Дано :
ΔАВС ~ ΔA₁В₁С₁.
Отношение сходственных сторон = .
.
S(ΔАВС) = S(ΔА₁В₁С₁) + 77 (см²).
Найти :
S(ΔАВС) = ?
S(ΔА₁В₁С₁) = ?
Отношение сходственных сторон подобных треугольников равно коэффициенту подобия.Отсюда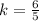 .
.
Так как k > 1, то в числителе стоит бо́льший треугольник.
Площади подобных треугольников относятся как квадрат коэффициента подобия.Пусть S(ΔА₁В₁С₁) = х, тогда S(ΔАВС) = х + 77 (см²) (так как площадь ΔАВС больше площади ΔА₁В₁С₁, то он, как раз таки, и есть бо́льший треугольник).
Составим уравнение -
S(ΔА₁В₁С₁) = x = 175 (cм²)
S(ΔАВС) = х + 77 (см²) = 175 (см²) + 77 (см²) = 252 (см²).
252 (см²), 175 (см²).
Площадь АВС в 3 в квадрате, то есть в 9 раз больше, чем площадь МВР.
Теперь берем треугольник МВР, а рядом рисуем АВС. МВ/АВ=1/3. Коэффициент подобия 1/3. Это значит, что первый треугольник меньше второго. Площадь МВР составляет 1/3 в квадрате или 1/9 часть площади АВС. Вот и все премудрости. Просто здесь важно стороны какого треугольника являются делимым, а какие делителем. Ведь в операции деления, в отличие от операции умножения, важен порядок.
А, находя коэффициенты подобия, мы именно делим!