У шаховому турнірі двоє учасників вибули, зігравши по три партії кожен, і тому на турнірі було зіграно усього 84 партії. Скільки було учасників спочатку?
Если центр описанной около треугольника окружности лежит внутри треугольника, значит треугольник остроугольный. Площадь треугольника равна половине произведения его сторон на синус угла между этими сторонами. В нашем случае S = (1/2)AB*BC*Sinα или 3√3 = 2√3*3*Sinα. Следовательно, Sinα = (3√3)/6√3 = 1/2. Итак, угол В в треугольнике АВС равен 30°. Cos30° = √3/2. По теореме косинусов находим сторону АС треугольника: АС = √(АВ²+ВС²-2*АВ*ВС*Cos30) или √(48+9-2*12√3*√3/2)=√21. Ну, а радиус описанной около треугольника окружности находится по формуле: R = a*b*c/4S или в нашем случае R=4√3*3*√21/12√3 = √21. ответ: радиус описанной около треугольника окружности равен √21.
Для плоского треугольника со сторонами a,b,c и углом α, противолежащим стороне a, справедливо соотношение:
Квадрат одной стороны треугольника равен сумме квадратов двух других сторон за вычетом удвоенного их произведения, умноженного на косинус угла между ними.
Доказательство теоремы косинусов
Рассмотрим произвольный треугольник ABC. Предположим, что нам известна величина стороны AC (она равна некому числу b), величина стороны AB (она равна некому числу c) и угол между этими сторонами, величина которого равна α. Найдем величину стороны BC (обозначив ее длину через переменную a)
Для доказательства теоремы косинусов проведем дополнительные построения. Из вершины C на сторону AB опустим высоту CD. Найдем длину стороны AB. Как видно из рисунка, в результате дополнительного построения можно сказать, что
Найдем длину отрезка AD. Исходя из того, что треугольник ADC является прямоугольным, нам известны длина его гипотенузы (b) и угол (α) то величину стороны AD можно найти из соотношения его сторон, пользуясь свойствами тригонометрических функций в прямоугольном треугольнике:
откуда
Длину стороны BD найдем как разность AB и AD:
Теперь запишем теорему Пифагора для двух прямоугольных треугольников ADC и BDC: для треугольника BDC
для треугольника ADC
Обратим внимание на то, что оба треугольника имеют общую сторону - CD. Определим ее длину для каждого треугольника - вынесем ее значение в левую часть выражения, а остальное - в правую.
Поскольку левые части уравнений (квадрат стороны CD) равны, то приравняем правые части уравнений:
Исходя из сделанных ранее вычислений, мы уже знаем что:
AC = b (по условию)
А значение стороны BC обозначим как a. BC = a (Именно его нам и нужно найти)
Получим:
Заменим буквенные обозначения сторон на результаты наших вычислений
перенесем неизвестное значение (а) на левую сторону, а остальные части уравнения - на правую
раскроем скобки
получаем
Теорема косинусов доказана.
Случай, когда один из углов при основании тупой (и высота падает на продолжение основания), полностью аналогичен рассмотренному.
Площадь треугольника равна половине произведения его сторон на синус угла между этими сторонами.
В нашем случае S = (1/2)AB*BC*Sinα или 3√3 = 2√3*3*Sinα.
Следовательно, Sinα = (3√3)/6√3 = 1/2.
Итак, угол В в треугольнике АВС равен 30°. Cos30° = √3/2.
По теореме косинусов находим сторону АС треугольника:
АС = √(АВ²+ВС²-2*АВ*ВС*Cos30) или
√(48+9-2*12√3*√3/2)=√21.
Ну, а радиус описанной около треугольника окружности находится по формуле: R = a*b*c/4S или в нашем случае R=4√3*3*√21/12√3 = √21.
ответ: радиус описанной около треугольника окружности равен √21.
Формулировка теоремы косинусов
Для плоского треугольника со сторонами a,b,c и углом α, противолежащим стороне a, справедливо соотношение:
Квадрат одной стороны треугольника равен сумме квадратов двух других сторон за вычетом удвоенного их произведения, умноженного на косинус угла между ними.
Доказательство теоремы косинусовРассмотрим произвольный треугольник ABC. Предположим, что нам известна величина стороны AC (она равна некому числу b), величина стороны AB (она равна некому числу c) и угол между этими сторонами, величина которого равна α. Найдем величину стороны BC (обозначив ее длину через переменную a)
Для доказательства теоремы косинусов проведем дополнительные построения. Из вершины C на сторону AB опустим высоту CD.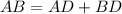
Найдем длину стороны AB. Как видно из рисунка, в результате дополнительного построения можно сказать, что
Найдем длину отрезка AD. Исходя из того, что треугольник ADC является прямоугольным, нам известны длина его гипотенузы (b) и угол (α) то величину стороны AD можно найти из соотношения его сторон, пользуясь свойствами тригонометрических функций в прямоугольном треугольнике:
откуда
Длину стороны BD найдем как разность AB и AD:
Теперь запишем теорему Пифагора для двух прямоугольных треугольников ADC и BDC:
для треугольника BDC
для треугольника ADC
Обратим внимание на то, что оба треугольника имеют общую сторону - CD. Определим ее длину для каждого треугольника - вынесем ее значение в левую часть выражения, а остальное - в правую.
Поскольку левые части уравнений (квадрат стороны CD) равны, то приравняем правые части уравнений:
Исходя из сделанных ранее вычислений, мы уже знаем что:
AC = b (по условию)
А значение стороны BC обозначим как a.
BC = a
(Именно его нам и нужно найти)
Получим:
Заменим буквенные обозначения сторон на результаты наших вычислений
перенесем неизвестное значение (а) на левую сторону, а остальные части уравнения - на правую
раскроем скобки
получаем
Теорема косинусов доказана.
Случай, когда один из углов при основании тупой (и высота падает на продолжение основания), полностью аналогичен рассмотренному.