ABCD-трапеция, BC и AD - основания
∠A = 90°, ∠D = 45°, BC = 4см, AB = 18см
BC
| | \
A||___\ D
E
Найти:
S(ABCD) - ?
Дополнительное построение: СЕ⊥AD
∠B = ∠A = ∠C = ∠E = 90° ⇒ ABCE - прямоугольник ⇒ AB = CE = 18см,
BC = AE = 4см
Рассмотрим ΔCED:
∠D = 45°
∠E = 90°
CE = 18 ⇒ ∠C = 90° - ∠D = ∠D = 45° ⇒ ΔCED -р/б ⇒ ED = CE =18см
AD = AE + ED = 4 + 18 = 22см
S(ABCD) = = = 234см²
S(ABCD) = 234см²
P.s: данные на чертёж заносить мне было проблематично, но это необходимо сделать. Мой чертёж чисто схематический, для представления фигуры создан.
Найти периметр трапеции по готовому чертежу
Объяснение:
∠BCО = ∠ОЕА= 30° как накрест лежащие , при секущей СЕ.
По т. о внешнем угле треугольника в ΔЕАО , ∠ЕОА=60°-30°=30°. Откуда ∠AOE = ∠BOC = 30° ⇒ ∠ВОС=30°.
Значит ΔЕАО=ΔСВО по стороне и 2-м прилежащим углам:
ОА=ОВ по условию,
∠AOE = ∠BOC = 30° ,
∠ЕАО=∠СВО как накрест лежащие ,АВ-секущая.
В равных треугольниках соответственные элементы равны ⇒ЕА=ВС.
Пусть ЕА=ВС=а. Т.к. ΔЕАО , ΔСВО-равнобедренные , то ЕА=ОА=ВС=ОВ=а . Тогда сторона трапеции АВ=2а ⇒ СD=2а (*),
т.к АВСD-равнобедренная трапеция( ∠D=180°-120°=60°)
Из Δ ECD -прямоугольный , ЕD=ЕА+АD=а+15 найдем CD = ED = (**).
Приравняем полученные выражения (*) и (**) , получим
2а = , 4а=а+15 , а=5 ⇒ ВС=5, АВ=СD=10
P(ABCD) = 5 + 15 +2* 10 =40 .
ABCD-трапеция, BC и AD - основания
∠A = 90°, ∠D = 45°, BC = 4см, AB = 18см
BC
| | \
A||___\ D
E
Найти:
S(ABCD) - ?
Дополнительное построение: СЕ⊥AD
∠B = ∠A = ∠C = ∠E = 90° ⇒ ABCE - прямоугольник ⇒ AB = CE = 18см,
BC = AE = 4см
Рассмотрим ΔCED:
∠D = 45°
∠E = 90°
CE = 18 ⇒ ∠C = 90° - ∠D = ∠D = 45° ⇒ ΔCED -р/б ⇒ ED = CE =18см
AD = AE + ED = 4 + 18 = 22см
S(ABCD) = = = 234см²
S(ABCD) = 234см²
P.s: данные на чертёж заносить мне было проблематично, но это необходимо сделать. Мой чертёж чисто схематический, для представления фигуры создан.
Найти периметр трапеции по готовому чертежу
Объяснение:
∠BCО = ∠ОЕА= 30° как накрест лежащие , при секущей СЕ.
По т. о внешнем угле треугольника в ΔЕАО , ∠ЕОА=60°-30°=30°. Откуда ∠AOE = ∠BOC = 30° ⇒ ∠ВОС=30°.
Значит ΔЕАО=ΔСВО по стороне и 2-м прилежащим углам:
ОА=ОВ по условию,
∠AOE = ∠BOC = 30° ,
∠ЕАО=∠СВО как накрест лежащие ,АВ-секущая.
В равных треугольниках соответственные элементы равны ⇒ЕА=ВС.
Пусть ЕА=ВС=а. Т.к. ΔЕАО , ΔСВО-равнобедренные , то ЕА=ОА=ВС=ОВ=а . Тогда сторона трапеции АВ=2а ⇒ СD=2а (*),
т.к АВСD-равнобедренная трапеция( ∠D=180°-120°=60°)
Из Δ ECD -прямоугольный , ЕD=ЕА+АD=а+15 найдем CD =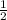 ED =
ED =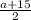 (**).
(**).
Приравняем полученные выражения (*) и (**) , получим
2а =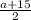 , 4а=а+15 , а=5 ⇒ ВС=5, АВ=СD=10
, 4а=а+15 , а=5 ⇒ ВС=5, АВ=СD=10
P(ABCD) = 5 + 15 +2* 10 =40 .