2)Т.к. АД║ВС ( основания трапеции), АС-секущая, то ∠ДАС=∠ВСА , как накрест лежащие. Значит в ΔАСВ есть два равных угла по 22,5° ⇒ ΔАСВ-равнобедренный и ВС=ВА=4√2.
3)Пусть ВК⊥АД, тогда ΔВКА-прямоугольный и равнобедренный , т.к. ∠КВА=90°-45°=45°. Обозначим равные катеты через х. По т. Пифагора :х²+х²=(4√2)², 2х²=16*2, х=4, КА=ВК=4.
Объяснение:
АВСД -прямоугольная трапеция ,ВС=4√2 , ∠А=45°, ∠Д=90°, АС-биссектриса ∠А.
1)Т.к АС-биссектриса, то ∠САД=∠САВ.
2)Т.к. АД║ВС ( основания трапеции), АС-секущая, то ∠ДАС=∠ВСА , как накрест лежащие. Значит в ΔАСВ есть два равных угла по 22,5° ⇒ ΔАСВ-равнобедренный и ВС=ВА=4√2.
3)Пусть ВК⊥АД, тогда ΔВКА-прямоугольный и равнобедренный , т.к. ∠КВА=90°-45°=45°. Обозначим равные катеты через х. По т. Пифагора :х²+х²=(4√2)², 2х²=16*2, х=4, КА=ВК=4.
3)Т.к. ВК⊥АД, то ДК=4√2.
4)ΔДВК-прямоугольный, по т. Пифагора ДВ²=КВ²+КД²,
ДВ²=16+16*2,
ДВ²=3*16
ДВ=4√3
Вариант 1.
Так как <ABC = 45°, то: <A = 90-45 = 45°.
И так как острые углы друг другу равны, то прямоугольный треугольник — равнобёдренный, тоесть: BC = AC.
//Росстояние от точки A — до плоскости "α" — это и есть катет AC.//
У нас есть 2 условия: AB+BC = 17; AC-BC = 7.
И так как эти 2 катета равны — то составим систему только с одной переменной "x":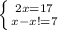
Э-э, стоп, что? Разность двух равных чисел не равна 7-и? Недопустимо!
Задача с ошибкой, если один и острых углов равен 45°, то второй тоже. Катеты равны, тоесть их разность не может быть равной 7-и.
Вариант 2.
Проигнорируем определение острого угла 45-градусов, представим, что нам известно только это: AC+BC = 17; AC-BC = 7.
Этой информации нам достаточно, чтобы найти катеты.
Но только на этот раз — переменных будет 2: AC = "x"; BC = "y".
Вывод: AC = 12.