Укажіть координати центра і радіус кола, заданого рівнянням (х+1)2+(у Все росписать и показать ответ я знаю проста не знаю как росписать. есль не тот ответ сори я кину реб.!!

a) Угол на нижнем треугольнике: 180-90-60=30

Треугольники равны по стороне и двум углам

б) Аналогично с (a). Угол на нижнем треугольнике: 180-90-50=40

Треугольники равны по стороне и двум углам.

в) В прямоугольном треугольнике, сторона, противолежащая углу в 30 равна половине гипотенузы. Следовательно:

на верхнем треугольнике гипотенуза равна 2*4 = 8

На нижнем треугольнике угол равен 30

Дальше можно найти третью сторону по теореме Пифагора и применить признак по трем сторонам, либо найти третий угол и применить признак по двум сторонам и углу между ними.

Нижняя сторона равна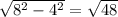

Верхний угол равен 180-90-30=60

Если что-то  непонятно - пишите, я уточню!

============

Не забывайте сказать " ", поставить оценку и, если ответ удовлетворил, то выберите его как "Лучший"

Бодрого настроения и добра!  

Успехов в учебе!

6.6

Объяснение:

Дан треугольник АВС. АВ=ВС=5.   АС=2.

Проведены высоты СК и AL .  Проведем также высоту ВН.

Найти периметр KLH.

АН=АС:2=1

По т Пифагора найдем ВН.

ВН= sqrt(AB²-AH²)=sqrt(25-1)=sqrt(24)

cos(ABH)=cos(B/2)=BH/AB= sqrt(24)/5

sin(B/2)=AH/AB=1/5

cos(B)=(cos(B/2))²-(sin(B/2))²=24/25-1/25=23/25

ΔCKB:     KB/CB=cos(B)

KB=CB*cos(B)=5*23/25=23/5

КВ=LB,  так как КB=BC/cos(B) и LB=AB/cos(B))  и   АВ=АС

=>Δ BKL- равнобедренный => ∡BKL=∡BLK

В треугольниках АВС и KBL угол В - общий.

=> ∡BKL=∡BAC=∡BLK=∡BCA=(180-∡B)/2

=> треугольники KBL и АВС подобны по 2-м углам

=> KB/AB=KL/AC

KL=23/25*2=46/25

Теперь из треугольника КНВ по т косинусов находим КН.

КН²=КВ²+НВ²-2*КВ*НВ*cos(B/2)

KH²=529/25+24-2*23*sqrt(24)*sqrt(24)/5/5

KH²=1129/25+46*24/5= (1129-1104)/25=1

KH=1

P(KLH)=KH+HL+KL=1+1+23/5=6.6