Умоляю Найдите значение выражения.
3х 2 -5х +4 при х=-1;
2.Представте в виде многочлена.
А.(6ху + 8у) – (2ху +9у – 2).
Б.5b(b-c) + c(2b – c)
В.(2х –у)(3у-4х)
Г.2c(3c – 5) – (c-3)(c-7)
3.(4х – 2у) 2 ;( х-у) 2 –х(х +2у)
4. Представить в виде квадрата двучлена.
4х 2 - 20ху + 25у 2

Показать ответ

Ответ:

ТыУмНыЙ

15.10.2020 13:12

∠С=30°,∠А=90°,∠В=60°

Объяснение:

Дано: AD⊥BC, ВО=ОС. ∠ВАD=∠DАО=∠ОАС

Найти: ∠А,∠В,∠С ΔАВС

Пусть ∠ВАD=∠DАО=∠ОАС=х

1) Рассмотрим ΔВАО. АD - высота. ∠ВАD=∠DАО ⇒ АD - биссектриса.

Если в треугольнике медиана совпадает с биссектрисой, то треугольник равнобедренный. ⇒ΔВАО - равнобедренный. В равнобедренном треугольнике высота является также медианой. ⇒

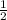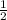ВD=DО= $\frac{1}{2}$ ВО= $\frac{1}{2}$ ОС.

2) Дополнительное построение: Проведём ОМ⊥АС.

Рассмотрим прямоугольные треугольники АDО и АМО.

∠DАО=∠ОАС - по условию, АО - общая.

Если гипотенуза и острый угол одного треугольника соответственно равны гипотенузе и острому углу другого треугольника, то такие прямоугольные треугольники равны.

⇒ΔАDО = ΔАМО

Из равенства треугольников следует равенство катетов:

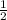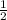DО = МО = $\frac{1}{2}$ ВО= $\frac{1}{2}$ ОС.

3) Рассмотрим прямоугольный треугольник ОМС (∠М=90°).

Из доказанного выше МО=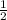 $\frac{1}{2}$ ОС. Т.е. катет МО равен половине гипотенузы ОС.

Если в прямоугольном треугольнике один из катетов равен половине гипотенузы, то этот катет лежит против угла в 30°.

Следовательно ∠С=30°

4) Рассмотрим прямоугольный треугольник АDC(∠D=90°).

По свойству острых углов прямоугольного треугольника

∠DАС=90°-∠С=90°-30°=60°.

По условию ∠DАС=2х ⇒ 2х=60°, х=30°

5) ∠ВАС=3х=3*30°=90°

∠А треугольника АВС = 90°

Так как сумма углов треугольника равна 180°, то ∠В треугольника АВС будет равен: ∠В=180°-∠А-∠С=180°-90°-30°=60°

Висота і медіана, проведені з однієї вершини трикутника,розділили його кут на три рівні частини. Зна

0,0(0 оценок)

Ответ:

strunets1

19.10.2021 00:37

Данные отрезки параллельны линии пересечения плоскостей, следовательно, параллельны друг другу. АВ║CD.

Расстоянием между параллельными прямыми является длина отрезка, проведенного перпендикулярно к обеим прямым.

Плоскость линейного угла по определению перпендикулярна ребру двугранного угла, значит, перпендикулярна и прямым, которые параллельны этому ребру. ⇒ отрезок АС, перпендикулярный АВ и CD, - искомое расстояние между АВ и CD.

Построим линейный угол МАС двугранного угла между данными плоскостями. В треугольнике АМС угол АМС равен 60°, и по т.косинусов:

квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.

АС²=8²+5*-2•8•5•cos60°

АС²=89-80•1/2

АС²=49

АС=√49=7 см - это ответ.