По определению, две прямые параллельны, если существует плоскость в которой лежат две эти прямые, и они там параллельны. Отметим на данной прямой точки A и B. А точку обозначим как O. Пусть через точку О проходят две прямые параллельные AB. Пусть -- плоскость, содержащая одновременно и AB (эта плоскость существует из определения). Аналогично определяем плоскость . Заметим, что и проходят через точки O, A, B. Но по аксиоме через три точки, не лежащие на одной прямой проходит только одна плоскость. Значит плоскости = S совпадают. (назовём их общим именем S). Рассмотрим плоскость S: в ней лежат точки O, A, B и две прямые . Причем, проходят через точку O и параллельны AB. Но по аксиоме планиметрии (напомню, мы сейчас живем в плоскости S для которой выполнены все аксиомы планиметрии) через точку O может проходить лишь одна прямая, параллельная AB. Значит , ч.т.д.
проекция Точки A на плоскость (A1B1C1)=A1, проекция точки D=D1, значит проекция отрезка AD=A1D1.
Отрезок A1D1║B1C1 из свойств правильного шестиугольника, и A1D1║AD так как плоскость (ABC)║(A1B1C1) значит AD║B1C1 Ч.Т.Д.
б)
Рассмотрим треугольник A1B1C1, опустим высоту A1H на основание B1C1, AH Также будет ⊥B1C1 по теореме о трех перпендикулярах, значит AH искомое расстояние.
AA1 будет ⊥A1H так-как он ⊥ плоскости (A1B1C1).
найдем A1H методом площадей в треугольнике A1B1C1.
Объяснение:
По определению, две прямые параллельны, если существует плоскость в которой лежат две эти прямые, и они там параллельны. Отметим на данной прямой точки A и B. А точку обозначим как O. Пусть через точку О проходят две прямые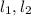 параллельные AB. Пусть
параллельные AB. Пусть 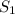 -- плоскость, содержащая одновременно
-- плоскость, содержащая одновременно 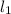 и AB (эта плоскость существует из определения). Аналогично определяем плоскость
и AB (эта плоскость существует из определения). Аналогично определяем плоскость 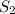 . Заметим, что
. Заметим, что 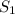 и
и 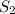 проходят через точки O, A, B. Но по аксиоме через три точки, не лежащие на одной прямой проходит только одна плоскость. Значит плоскости
проходят через точки O, A, B. Но по аксиоме через три точки, не лежащие на одной прямой проходит только одна плоскость. Значит плоскости 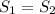 = S совпадают. (назовём их общим именем S). Рассмотрим плоскость S: в ней лежат точки O, A, B и две прямые
= S совпадают. (назовём их общим именем S). Рассмотрим плоскость S: в ней лежат точки O, A, B и две прямые 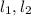 . Причем,
. Причем, 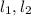 проходят через точку O и параллельны AB. Но по аксиоме планиметрии (напомню, мы сейчас живем в плоскости S для которой выполнены все аксиомы планиметрии) через точку O может проходить лишь одна прямая, параллельная AB. Значит
проходят через точку O и параллельны AB. Но по аксиоме планиметрии (напомню, мы сейчас живем в плоскости S для которой выполнены все аксиомы планиметрии) через точку O может проходить лишь одна прямая, параллельная AB. Значит 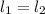 , ч.т.д.
, ч.т.д.
а)
проекция Точки A на плоскость (A1B1C1)=A1, проекция точки D=D1, значит проекция отрезка AD=A1D1.
Отрезок A1D1║B1C1 из свойств правильного шестиугольника, и A1D1║AD так как плоскость (ABC)║(A1B1C1) значит AD║B1C1 Ч.Т.Д.
б)
Рассмотрим треугольник A1B1C1, опустим высоту A1H на основание B1C1, AH Также будет ⊥B1C1 по теореме о трех перпендикулярах, значит AH искомое расстояние.
AA1 будет ⊥A1H так-как он ⊥ плоскости (A1B1C1).
найдем A1H методом площадей в треугольнике A1B1C1.
$$\begin{lgathered}S=\frac{1}{2} A_1B_1*B_1C_1*sin(120)=\frac{1}{2} B_1C_1*A_1H\\a^2*sin(120)=a*A_1H\\A_1H=a*sin(180-60)=a*sin(60)=\frac{a\sqrt{3}}{2}\end{lgathered}$$
A1H также можно было найти рассмотрев треугольник A1BH, сказав что A1H=A1B1*sin(60)
теперь по теореме пифагора найдем AH:
$$AH=\sqrt{A_1H^2+AA_1^2}=\sqrt{\frac{4a^2}{4}+\frac{3a^2}{4}}=\frac{a\sqrt{7}}{2}$$
ответ: $$AH=\frac{a\sqrt{7}}{4}$$