В ∆ АВС, b=6√2 см, кут А=15°, кут С=45°. Найти С

Question

Геометрия: В ∆ АВС, b=6√2 см, кут А=15°, кут С=45°. Найти С​

sveta19772011owor7w · Answer

ЕСли АВСД - прямоугольник,

1)значит пара сторон(векторов) параллельны АВ(3-4;5-1)=АВ(-1;4)

ДС(-1-0;4-0)=ДС(-1;4)

Чтобы найти координаты вектора из координат конца вектора вычел координаты начала АВ=ДС (это векторы) раз координаты векторов равны то и векторы равны значит параллельны

2)Диагонали прямоугольника равны) - это уже длины

Сначала найду координаты векторов: АС(-1-4;4-1)=АС(-5;3)

ВД(0-3;0-5) =ВД(-3;-5)

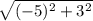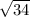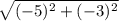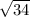
Теперь найду длину АС= $\sqrt{(-5)^2+3^2}$ = $\sqrt{34}$ ВД= $\sqrt{(-5)^2+(-3)^2}$ = $\sqrt{34}$

Так как АВ|| ДС; AB= СД; АС=ВД - это АВСД прямоугольник

Объяснение:

В ∆ АВС, b=6√2 см, кут А=15°, кут С=45°. Найти С​