AC (х+2)/(7+2)=(у+2)/(7+2), после преобразований получается у=х или х-у=0.
BD (х+3)/(3+3)=(у-1)/(1-1). Вот что делает формальный подход. После преобразований получается: (х+3)/6=(у-1)/0. Ужас! деление на ноль! А всего лишь, нужно было внимательнее посмотреть и осмыслить значения. У точек B и D одинаковые ординаты. А это значит, что BD - горизонтальная линия, и ее уравнение у=1.
Теперь нужно выяснить, какие же линии - основания, а какие - боковые стороны.
Конечно, если мы начертим трапецию, то сразу видно, что AD параллельно ВС, значит что ADи ВС - основания. Но ведь нам нужно обойтись без чертежа. Значит придется составить уравнения АВ, ВС, CD и АD, и выбрать из них две с одинаковыми коэффициентами.
Итак: (на всякий случай пока отправлю то, что есть, так как с минуты на минуту может прийти жена, и выгонит меня из-за компа).
Видим, что одинаковые угловые коэффициенты (при х) у линий BC и AD. Значит это основания.
Теперь главная фишка. Можно было бы тупо вычислить координаты точек на серединах сторон АВ и СD и написать уравнение линии, проходящей через эти точки.
Но, поскольку средняя линия параллельна основаниям, то угловой коэффициент у нее одинаков с ними, т.е. 0,6. Так как она проходит посередине между ними, то свободный член уравнения равен среднему арифметическому свободных членов уравнений BD и АС, т.е (2,8-0,8)/2=1. Получаем уравнение средней линии у=0,6х+1.
Найдём координаты центра окружности, используя правило нахождения среднего арифметического чисел.
Т.е. возьмём у точки "A" и точки "B" координату по оси абсцисс (Ox). Представьте, что мы должны найти среднее арифметическое чисел "6" и "-2".
Вспоминаем правило: чтобы найти среднее арифметическое, нужно сложить все числа и поделить их сумму на их количество (пример прикреплён ниже).
Теперь поработаем с выбранными координатами точек:
.
Теперь мы знаем, что за координата указана по оси абсцисс. Но нам ещё нужно найти координату по оси ординат (Oy).
Делаем всё по аналогии нахождения координаты оси абсцисс. Берём вторые координаты у обоих точек, которые образуют отрезок "AB". Это будут координаты "-7" и "5". Теперь находим их среднее арифметическое и получаем ответ:
ответ: у=0,6х+1.
Объяснение:
Уравнения диагоналей:
AC (х+2)/(7+2)=(у+2)/(7+2), после преобразований получается у=х или х-у=0.
BD (х+3)/(3+3)=(у-1)/(1-1). Вот что делает формальный подход. После преобразований получается: (х+3)/6=(у-1)/0. Ужас! деление на ноль! А всего лишь, нужно было внимательнее посмотреть и осмыслить значения. У точек B и D одинаковые ординаты. А это значит, что BD - горизонтальная линия, и ее уравнение у=1.
Теперь нужно выяснить, какие же линии - основания, а какие - боковые стороны.
Конечно, если мы начертим трапецию, то сразу видно, что AD параллельно ВС, значит что ADи ВС - основания. Но ведь нам нужно обойтись без чертежа. Значит придется составить уравнения АВ, ВС, CD и АD, и выбрать из них две с одинаковыми коэффициентами.
Итак: (на всякий случай пока отправлю то, что есть, так как с минуты на минуту может прийти жена, и выгонит меня из-за компа).
Продолжаю.
Уравнения сторон:
АВ (х+2)/(-3+2)=(у+2)/(1+2), 3х+6=-у-2, у=-3х-8;
ВС (х+3)/(7+3)=(у-1)/(7-1), 6х+18=10у-10, у=0,6х+2,8;
СD (DC) (х-3)/(7-3)=(у-1)/(7-1), 6х-18=4у-4, у=1,5х-3,5;
AD х+2/(3+2)=(у+2)/(1+2), 3х+6=5у+10, у=0,6х-0,8.
Видим, что одинаковые угловые коэффициенты (при х) у линий BC и AD. Значит это основания.
Теперь главная фишка. Можно было бы тупо вычислить координаты точек на серединах сторон АВ и СD и написать уравнение линии, проходящей через эти точки.
Но, поскольку средняя линия параллельна основаниям, то угловой коэффициент у нее одинаков с ними, т.е. 0,6. Так как она проходит посередине между ними, то свободный член уравнения равен среднему арифметическому свободных членов уравнений BD и АС, т.е (2,8-0,8)/2=1. Получаем уравнение средней линии у=0,6х+1.
Диаметр окружности: отрезок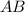 .
.
Центр окружности: точка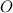 .
.
Координаты следующих точек: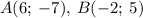 .
.
Найти нужно координаты центра окружности: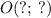 .
.
Решение:Найдём координаты центра окружности, используя правило нахождения среднего арифметического чисел.
Т.е. возьмём у точки "A" и точки "B" координату по оси абсцисс (Ox). Представьте, что мы должны найти среднее арифметическое чисел "6" и "-2".
Вспоминаем правило: чтобы найти среднее арифметическое, нужно сложить все числа и поделить их сумму на их количество (пример прикреплён ниже).
Теперь поработаем с выбранными координатами точек:
Теперь мы знаем, что за координата указана по оси абсцисс. Но нам ещё нужно найти координату по оси ординат (Oy).
Делаем всё по аналогии нахождения координаты оси абсцисс. Берём вторые координаты у обоих точек, которые образуют отрезок "AB". Это будут координаты "-7" и "5". Теперь находим их среднее арифметическое и получаем ответ:
(чертёж к задаче прикреплён ниже)
ответ: