В параллелепипеде ABCDA1B1C1D1, АВСД - квадрат со стороной, равной 2 см. Все боковые грани -прямоугольники, В1Д = 5 см. Найти углы между В1Д и плоскостью АВС и междуВ1Д и плоскостью ДД1С1

Если в условии имеется в виду, что  отрезок каждой длины можно использовать в четырехугольнике только один раз, то ни одного 4-угольника составить нельзя. Действительно, пусть длины сторон четырехугольника равны 2^k, 2^l, 2^m, 2^n, где 0≤k<l<m<n≤6. Тогда должно выполняться 2^k+2^l+2^m>2^n, т.к. длина ломаной всегда больше расстояния между ее конечными точками. Но 2^k+2^l+2^m≤2^(m-2)+2^(m-1)+2^m=
=2^(m-2)*(1+2+4)=7*2^(m-2)<2^(m+1)≤2^n. Т.е. получается, что сумма трех меньших сторон четырехугольника меньше большей стороны. Противоречие. Т.е. четырехугольника с  различными сторонами с длинами из этого списка не существует.

Если допустить, что некоторые длины сторон могут повторяться, то различных четырехугольников можно составить бесконечно много, т.к. даже со сторонами 1,1,1,1 существует бесконечное число различных ромбов.

Задание 1

ответ: Да, существует. Это правильный 8-ми угольник (см. картинку №1).

Объяснение:

Известно что сумма внутренних углов выпуклого многоугольника S равна произведению 180° на количество сторон n без двух:

S = 180°(n-2)

Т.к. сумма внутренних углов выпуклого многоугольника = внутреннему углу, помноженному на количество сторон ⇒

S = 135° × n

Отсюда выходит что:

135n = 180(n-2)

Находим n:

135n = 180n - 360

180n - 135n = 360

45n = 360

n = 360 ÷ 45

n = 8 (количество сторон правильного многоугольника)

Задание 2

ответ: Количество сторон правильного многоугольника = 12 (см. картинку №2).

Объяснение:

Пускай внутренний угол правильного многоугольника = x°

⇒ смежный с ним угол = 0,2x°

Смежные углы — это пара углов, у которых одна сторона общая, а две другие стороны лежат на одной прямой. Следовательно, два смежных угла составляют развёрнутый угол = 180°.

⇒ x + 0,2x = 180

1,2x = 180

x = 180 ÷ 1,2

x = 150° (внутренний угол выпуклого многоугольника)

Известно что сумма внутренних углов выпуклого многоугольника S равна произведению 180° на количество сторон n без двух:

S = 180°(n-2)

Т.к. сумма внутренних углов выпуклого многоугольника = внутреннему углу, помноженному на количество сторон ⇒

S = 150° × n

Отсюда выходит что:

150n = 180(n-2)

Находим n:

150n = 180n - 360

180n - 150n = 360

30n = 360

n = 360 ÷ 30

n = 12 (количество сторон правильного многоугольника)

Задание 3

а) ответ: Площадь многоугольника = 64 см².

Объяснение:

Правильный многоугольник, в котором n = 4 это КВАДРАТ.

Диаметр окружности d = 2r, где r - радиус

Известно что сторона квадрата a равна диаметру d вписанной в него окружности

⇒ d = a = 2r = 2×4 = 8 cm.

Площадь квадрата = a² = 8² = 64 cm²

б) ответ: Радиус вписанной окружности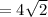 см.

Объяснение:

Известно что сторона квадрата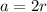 , где r - радиус вписанной окружности.

Так же известно что сторона квадрата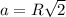 , где R - радиус описанной окружности ⇒

(радиус вписанной окружности)

в) ответ: Периметр многоугольника = 16 см.

Объяснение:

Известно что сторона квадрата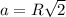 , где R - радиус описанной окружности

⇒

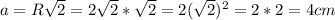
Периметр любого многоугольника P = n·a, где a - сторона многоугольника, n - количество его сторон.

⇒ P = 4 × 4 = 16 cm