В параллелограмме ABСD сторона AC=(корень из 2)*AB. Докажите, что углы между сторонами параллелограмма равны углам между диагоналями параллелограмма. на спам подаю жалобу
Решением треугольника называется нахождение всех его шести элементов (т. е. трех сторон и трех углов) по каким-нибудь трем данным элементам, определяющим треугольник.
Нехай задана правильна трикутна призма, бічні грані якої є квадратами, а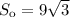 см² — площа основи цієї призми.
см² — площа основи цієї призми.
Основа призми є правильним (рівностороннім) трикутником зі строною см. Знайдемо цю сторону, скориставшись площею рівностороннього трикутника:
см. Знайдемо цю сторону, скориставшись площею рівностороннього трикутника: 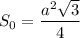
Отже,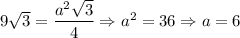 см.
см.
Через те що бічні грані є квадратами, тоді ребра призми дорівнюють 6 см (за властивістю квадрата) — ребра правильної призми є висотою призми.
Об'єм правильної трикутної призми можна розрахувати за формулою
Знайдено значення шуканої величини:
Відповідь: А)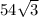 см³
см³
Решением треугольника называется нахождение всех его шести элементов (т. е. трех сторон и трех углов) по каким-нибудь трем данным элементам, определяющим треугольник.
Из суммы углов треугольника найдем угол С:
∠С=180º-45º-60º=75º
В прямоугольном ⊿ ВНС угол ВСН=90º-45º=45º
⊿ ВНС - равнобедренный, СН=ВН=ВС•sin 45º=(√3•√2):2
В ⊿ АНС сторона АС=СH:sin 60º
AC=[(√3•√2):2]:(√2):2=√2
АВ=ВН+АН
АН противолежит углу НСА, равному 90º-60º=30º
АН=АС:2=(√2):2
АВ=(√3•√2):2+(√2):2=(√3+1):√2
––––––––––––
Или по т. синусов:
АВ:sin75=BC:sin60
sin 60º=(√3):2
sin 75º=(√3+1):2√2 ( из таблицы тригонометрических функций)
АВ:(√3+1):2√2=(√3):[(√3):2]⇒
AB=(√3+1):√2
--------------
или по т.косинусов
AB²=BC²+AC²- 2BC•AC•cos75º
cos 75º=(√3-1):2√2
AB²=3+2- 2√6•((√3-1):2√2)⇒
AB=√(2+√3)
Оба найденных значения АВ равны - проверьте, возведя их в квадрат.
[√(2+√3)]²=[(√3+1):√2]²