В правильній чотирикутній піраміді ребро основи дорівнює 3√6 см. Об’єм піраміди 54 см. Знайти висоту піраміди і радіус кола, описаного навколо основи.
1. Площади подобных треугольников относятся как квадрат коэффициента подобия.
Т.к. стороны A₁ B₁ C₁ в 2 раза меньше сторон ABC, то коэффициент подобия равен 2, =>
(см²)
2) Пусть сторона большого куба равна , тогда по условию сторона меньшего куба равна .
Объем большого куба: (см³)
Объем меньшего куба: (см³)
3) Матрешку можно рассматривать как цилиндр.
Формула массы цилиндра: - плотность материала, - объем цилиндра.
Формула объема цилиндра: - радиус основания, - высота цилиндра.
Если меньшая матрешка вдвое меньше большей, то делаем вывод что высота большей матрешки вдвое больше высоты меньшей матрешки, а также радиус основания большей матрешки вдвое больше радиуса основания меньшей матрешки.
Пусть - радиус основания меньшей матрешки, - высота меньшей матрешки, тогда по формуле:
1) 25
2) 15,625
3)1,2
Объяснение:
1. Площади подобных треугольников относятся как квадрат коэффициента подобия.
Т.к. стороны A₁ B₁ C₁ в 2 раза меньше сторон ABC, то коэффициент подобия равен 2, =>
2) Пусть сторона большого куба равна , тогда по условию сторона меньшего куба равна
, тогда по условию сторона меньшего куба равна 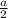 .
.
Объем большого куба: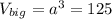 (см³)
(см³)
Объем меньшего куба: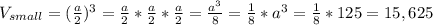 (см³)
(см³)
3) Матрешку можно рассматривать как цилиндр.
Формула массы цилиндра: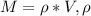 - плотность материала,
- плотность материала, 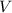 - объем цилиндра.
- объем цилиндра.
Формула объема цилиндра: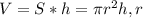 - радиус основания,
- радиус основания, 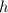 - высота цилиндра.
- высота цилиндра.
Если меньшая матрешка вдвое меньше большей, то делаем вывод что высота большей матрешки вдвое больше высоты меньшей матрешки, а также радиус основания большей матрешки вдвое больше радиуса основания меньшей матрешки.
Пусть - радиус основания меньшей матрешки,
- радиус основания меньшей матрешки, 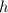 - высота меньшей матрешки, тогда по формуле:
- высота меньшей матрешки, тогда по формуле:
1) нет
2) да
3) нет
4) нет
5) нет
6) нет
7) нет
8) нет
9) нет; да
10) да
11) нет; да
13) да
14) нет
15) 16) да; да
Объяснение:
Параллелограмм - четырехугольник, у которого стороны попарно паралелльны
Свойства параллелограмма:
1) Противолежащие стороны и углы равны
2) Диагонали точкой пересечения делятся попол
ам
3) Биссектриса угла параллелограмма образует р/б ∆
Прямоугольник - параллелограмм, у которого все углы прямые
Свойства прямоугольника:
Те же, что и у параллелограмма 1) 2)
4) Диагонали прямоугольника равны
Ромб - параллелограмм, у которого все стороны равны
Свойства ромба:
Те же, что и у параллелограмма 1) 2)
5) Диагонали ромба взаимно перпендикулярны и делят его углы пополам
Квадрат - прямоугольник, у которого все стороны равны
Свойства квадрата:
Те же, что и прямоугольника и ромба 1) 2) 4) 5)