В прямокутнику ABCD діагональ ділить кут у відношенні 1:4. Визначити гострий кут між діагоналями. варінти відповіді:
1) 36
2)28
3)18
4)72

Показать ответ

Ответ:

эля792

18.03.2020 06:08

$3\sqrt{89}$

Объяснение:

Объём пирамиды:

$V=\frac{1}{3} S*h$ , где S - площадь основания, h - высота пирамиды.

Значит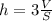 $h=3\frac{V}{S}$

У правильной четырёхугольной пирамиды основанием выступает квадрат. Если сторону квадрата обозначить как а, то S=a² ⇒ а=√S.

Боковое ребро пирамиды l, её высота h и полудиагональ основания образуют прямоугольный треугольник, в котором искомое ребро - гипотенуза, а высота и полудиагональ - катеты.

Диагональ квадрата равна √(2а²)=а*√2,

тогда половина диагонали равна а/√2, а так как а=√S,

то половина диагонали равна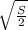 $\sqrt{\frac{S}{2} }$

Тогда, по теореме Пифагора:

$l=\sqrt{\frac{S}{2}+(3\frac{V }{S})^{2} }\\l=\sqrt{72+27^{2} } =\sqrt{72+729} =\sqrt{801} =3\sqrt{89}$

0,0(0 оценок)

Ответ:

YNOCHKA2008

18.03.2020 06:08

Пусть есть 2 пересекающиеся прямые, КМ и РТ. Точку их пересечения обозначим О. По трем точкам - КРО или МТО можно построить только одну плоскость. Поскольку точки К и М лежат на одной прямой, а Р и Т тоже на одной прямой, то обе этих прямых целиком принадлежат этой плоскости.
Значит, плоскость КРО совпадает с плоскостью МТО, то есть обе прямые лежат в одной плоскости.
Значит, все 4 точки лежат в одной плоскости, а это противоречит условию.
Вывод: Если 4 точки не лежат в одной плоскости, то прямые, их соединяющие попарно, скрещивающиеся.

0,0(0 оценок)

Популярные вопросы: Геометрия