Так как высоты равнобедренного треугольника, проведенные к боковым сторонам, равны, то можем рассмотреть только высоту CE.
Отрезок СК виден из точек Е и М под прямым углом, поэтому четыр-ник СМКЕ можно вписать в окружность. Это ключевой факт в этой задаче. Дальше просто считаем.
∠КЕМ = ∠КСМ = 25° - углы опираются на общую дугу КМ
Так как высоты равнобедренного треугольника, проведенные к боковым сторонам, равны, то можем рассмотреть только высоту CE.
Отрезок СК виден из точек Е и М под прямым углом, поэтому четыр-ник СМКЕ можно вписать в окружность. Это ключевой факт в этой задаче. Дальше просто считаем.
∠КЕМ = ∠КСМ = 25° - углы опираются на общую дугу КМ
∠МЕС = 90° - ∠КЕМ = 90° - 25° = 65°
СЕ = СМ - по условию ⇒ ΔСЕМ - равнобедренный
∠ЕСМ = 180° - 65° - 65° = 50°
В ΔВЕС ∠ЕВС = 90° - ∠ЕСВ = 90° - 50° = 40°
∠ВАС = ∠ВСА = (180° - 40°)/2 = 70°
Объяснение:
Назовем α плоскость M₁N₁P₁
Назовем β плоскость M₁QP₁
очка Q₁ также принадлежит α. (Можно доказать различными
Проведем Q₁N₁
Диагонали квадрата пересекаются под прямым углом и точкой пересечения делятся пополам.
Значит Q₁H ⊥ M₁P₁
Q₁H =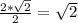
QQ₁ ⊥ α т.к QQ₁ ⊥ M₁Q₁ и QQ₁ ⊥ P₁Q₁
QH ⊥ M₁P₁ по Т. о трех перпендикулярах (QQ₁ - перпендикуляр, QH-наклонная, Q₁H - проекция)
∠(α,β) = ∠Q₁HQ
tan(∠(α,β)) = tan(∠Q₁HQ) =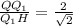
============
Не забывайте нажать " ", поставить оценку и, если ответ удовлетворил, то выберите его как "Лучший"
Бодрого настроения и добра!
Успехов в учебе!