В треугольнике ABC угол C прямой, угол А = 60°, AB = 28 см. Проведена окружность с центром в точке A. Каким должен быть её радиус, чтобы она касалась прямой BC. ответ дайте в сантиметрах. варианты ответов: 12см, 13см, 15см, 14см.
По свойству касательной к окружности она должная быть перпендикулярна радиусу. В данном случае т.к. AС ⊥ BC (по условию ∠С = ) и центр окружности в точке А, то АС и есть тот радиус, который нужно найти.
Но АС лежит напротив угла B, а ∠B = - ∠A = , таким образом ∠B =
Известно, что катет, лежащий напротив угла равен половине гипотенузы/
AB - гипотенуза и по условию AB = 28, ⇒ AC = 28 : 2 = 14 (см)
14 см
Объяснение:
По свойству касательной к окружности она должная быть перпендикулярна радиусу. В данном случае т.к. AС ⊥ BC (по условию ∠С =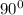 ) и центр окружности в точке А, то АС и есть тот радиус, который нужно найти.
) и центр окружности в точке А, то АС и есть тот радиус, который нужно найти.
Но АС лежит напротив угла B, а ∠B =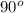 - ∠A =
- ∠A = 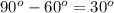 , таким образом ∠B =
, таким образом ∠B = 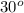
Известно, что катет, лежащий напротив угла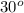 равен половине гипотенузы/
равен половине гипотенузы/
AB - гипотенуза и по условию AB = 28, ⇒ AC = 28 : 2 = 14 (см)