Для нахождения производной, воспользуемся двумя формулами:
1) при нахождении производной разности, нужно помнить, что производная разности равна разности производных. (u - v)' = u' - v'. Если немного запутано, то когда будешь смотреть пример, то, думаю, поймёшь. 2) ( 3) (cosx)' = - sinx
Сначала перепишем за знак производной константу 2 (2 - число, которое не может просто взять и измениться само по себе - константа) и поставим знак умножения, дальше нас интересует нахождение производной от . По формуле, которую я записала выше, мы можем увидеть, что показатель степени 6 мы записываем перед х (становится множителем), но х не остаётся без показателя степени, по формуле записано n - 1, то есть в нашем случае это 6 - 1 ( = 5), то есть х становится в 5й степени.
С косинусом даже легче: производная косинуса (по формуле) равна синусу, но обязательно со знаком минус, т.е. - sinx
Третий момент, на который нужно обратить внимание, - то, что перед косинусом первоначально был минус. При нахождении производной получается - (-sinx), если перед скобкой стоит минус, то знак в скобках меняется, поэтому в ответе становится + sinx.
Объём правильной четырёхугольной пирамиды: V=(1/3)a²h где а - сторона квадрата, основания пирамиды, h - высота пирамиды. Чтобы найти объём надо найти высоту пирамиды. Рассмотрим точку пересечения диагоналей квадрата. В эту точку опущена высота пирамиды, обозначим её О. Вершины квадрата обозначим АВСD, а вершину пирамиды S. В треугольнике АSO стороны AS - ребро пирамиды, SO - высота пирамиды, АО - половина диагонали основания пирамиды. Так как основание правильной пирамиды квадрат, а диагонали квадрата пересекаются под прямым углом, можем найти катеты АО и ВО прямоугольного равнобедренного треугольника АОВ по теореме Пифагора: AB²=AO²+BO², так как АО=ВО AB²=2AO² отсюда находим АО²=АВ²/2=6²/2=36/2=18 ⇒ АО=√18 Теперь можем найти высоту SO опять же по теореме Пифагора: AS²=SO²+AO² SO²=AS²-AO²=(√82)²-(√18)²=82-18=64 SO=8 Осталось найти объём V=(1/3)*6²*8=96
y' = 12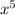
+ sinx
Объяснение:
Для нахождения производной, воспользуемся двумя формулами:
1) при нахождении производной разности, нужно помнить, что производная разности равна разности производных. (u - v)' = u' - v'. Если немного запутано, то когда будешь смотреть пример, то, думаю, поймёшь. 2) (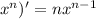
3) (cosx)' = - sinx
у = 2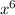
- cosx
y' = (2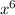
- cosx)' = (2 · 
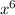)' - (cosx)' = 2 · (
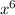)' - (cosx)' = 2 · 6
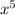- (-sinx) = 12
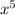+ sinx
Попробую ещё немного объяснить:
Как получить производную от 2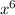
Сначала перепишем за знак производной константу 2 (2 - число, которое не может просто взять и измениться само по себе - константа) и поставим знак умножения, дальше нас интересует нахождение производной от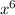
. По формуле, которую я записала выше, мы можем увидеть, что показатель степени 6 мы записываем перед х (становится множителем), но х не остаётся без показателя степени, по формуле записано n - 1, то есть в нашем случае это 6 - 1 ( = 5), то есть х становится в 5й степени.
С косинусом даже легче: производная косинуса (по формуле) равна синусу, но обязательно со знаком минус, т.е. - sinx
Третий момент, на который нужно обратить внимание, - то, что перед косинусом первоначально был минус. При нахождении производной получается - (-sinx), если перед скобкой стоит минус, то знак в скобках меняется, поэтому в ответе становится + sinx.
Если ещё есть вопросы, задавай в комментариях.
V=(1/3)a²h
где а - сторона квадрата, основания пирамиды, h - высота пирамиды.
Чтобы найти объём надо найти высоту пирамиды. Рассмотрим точку пересечения диагоналей квадрата. В эту точку опущена высота пирамиды, обозначим её О. Вершины квадрата обозначим АВСD, а вершину пирамиды S. В треугольнике АSO стороны AS - ребро пирамиды, SO - высота пирамиды, АО - половина диагонали основания пирамиды.
Так как основание правильной пирамиды квадрат, а диагонали квадрата пересекаются под прямым углом, можем найти катеты АО и ВО прямоугольного равнобедренного треугольника АОВ по теореме Пифагора:
AB²=AO²+BO², так как АО=ВО AB²=2AO² отсюда находим
АО²=АВ²/2=6²/2=36/2=18 ⇒ АО=√18
Теперь можем найти высоту SO опять же по теореме Пифагора:
AS²=SO²+AO²
SO²=AS²-AO²=(√82)²-(√18)²=82-18=64
SO=8
Осталось найти объём
V=(1/3)*6²*8=96
ответ: 96