В треугольнике CDE угол С=30°, угол D=50°. Найдите внешний угол треугольника. Сделайте чертёж

Показать ответ

Ответ:

281120057

24.11.2020 03:48

<X=<80=80 градусов,как накрест лежащие

<У+<80=180 градусов,как односторонние

<У=180-80=100 градусов

Номер 2

Прямые а и b параллельны,т к накрест лежащие углы равны между собой(при секущей М)

<52+<PEF=180 градусов,как односторонние

<РЕF=180-52=128 градусов

<Х=<РЕF=128 градусов,как вертикальные

Номер 3

а и b параллельные прямые при секущей В,т к накрест лежащие углы равны между собой

<Х=<40=40 градусов,как соответственные

<Х+<У=180 градусов,как смежные

<У=180-40=140 градусов

Объяснение:

0,0(0 оценок)

Ответ:

поать

24.11.2020 03:48

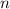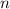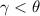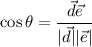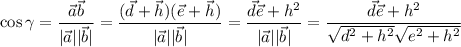Многогранный угол составлен боковыми сторонами -угольной пирамиды, в основании которой лежит выпуклый -угольник. Рассмотрим одну из таких сторон. Докажем, что $\gamma$ (см. рисунок). Тогда $\cos\theta = \dfrac{\vec{d}\vec{e}}{|\vec{d}||\vec{e}|}$ и $\cos\gamma = \dfrac{\vec{a}\vec{b}}{|\vec{a}||\vec{b}|} = \dfrac{(\vec{d}+\vec{h})(\vec{e}+\vec{h})}{|\vec{a}||\vec{b}|} = \dfrac{\vec{d}\vec{e}+h^2}{|\vec{a}||\vec{b}|} = \dfrac{\vec{d}\vec{e}+h^2}{\sqrt{d^2+h^2}\sqrt{e^2+h^2}}$ . Вот сейчас будет немного муторно: 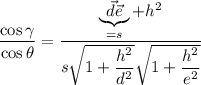$\dfrac{\cos\gamma}{\cos\theta} = \dfrac{\underbrace{\vec{d}\vec{e}}_{=s}+h^2}{s\sqrt{1+\dfrac{h^2}{d^2}}\sqrt{1+\dfrac{h^2}{e^2}}}$ . Однако 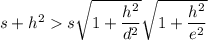$s+h^2 s\sqrt{1+\dfrac{h^2}{d^2}}\sqrt{1+\dfrac{h^2}{e^2}}$ , действительно, 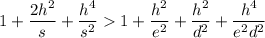$1+\dfrac{2h^2}{s}+\dfrac{h^4}{s^2}1+\dfrac{h^2}{e^2}+\dfrac{h^2}{d^2}+\dfrac{h^4}{e^2d^2}$ , что верно, поскольку каждое слагаемое слева (кроме единицы) больше соответствующего слагаемого справа. Поэтому 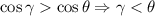$\cos\gamma \cos\theta \Rightarrow \gamma$ . Теперь спроецировав вершину 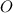многогранного угла на плоскость (многоугольник), получим, что сумма плоских углов меньше суммы углов при вершине 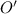проекции 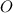, которая равна в точности 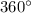$360^{\circ}$ , что и требовалось.