Використовуючи рис. 1, установіть відповідність між умовами задач (1-4) і відповідями до них (А-Д). 1 Знайдіть КР, якщо діаметр NP=10 а кут а дорівню 60 2 Знайдіть КР, якщо <NОА=<АОК ><KOP, NP-12 3 Знайдіть AN, якщо NC-Co. АС=СВ. R=4 4 Bakairs NC, axmo R-6, 20AC-30°, NPLAB A3 B5 Г2 Д6
Диагональ равнобокой трапеции ABCD перпендикулярна боковой стороне. Радиус окружности описанной около трапеции равен R=5 , ВС=6 . Найти площадь трапеции .
Объяснение:
Все вершины трапеции лежат на окружности , в том числе вершины
Δ АCD - прямоугольного, значит центр описанной окружности лежит на середине гипотенузы AD . Поэтому AD=2*R=2*5=10 (ед. изм.).
Пусть ВН⊥AD ,CK⊥AD , тогда НВСК-прямоугольник и ВС=НК=6 (ед.изм.).
Тогда КD=(AD-HK):2=(10-6):2=2( ед.изм.), Тогда АК=10-2=8 (ед.изм.)
Δ АCD -прямоугольный , т.к. высота, проведенная из вершины прямого угла, равна среднему геометрическому проекций катетов на гипотенузу, то СК=√(2*8)=4 (ед.изм.)
S(ABCD)=1/2*CK*(AD+BC)
S(ABCD)=1/2*4*(6+10)=32(ед.изм.²)
ABCD - квадрат со стороной, равной α, BM ⊥ ABC, BM = α. Найдите двугранный угол, образованный гранями AMD и CMD.
Объяснение:
1) Пусть АР⊥MD, соединим Р и С.
Т.к. АВ⊥AD, то по т. о трех перпендикулярах МА⊥AD⇒ΔAMD-прямоугольный. Т.к. ВС⊥СD, то по т. о трех перпендикулярах МС⊥CD ⇒ΔCMD-прямоугольный
2) Прямоугольные ΔAMD=ΔCMD по катету ( AD=CD стороны квадрата) и гипотенузе (MD--общая), значит и СР⊥MD, Поэтому ∠АРС-линейный угол двугранного , образованный гранями AMD и CMD.
3 ) Применим т. косинусов для ΔАРС :
АС²=АР²+РС²-2*АР*РС*cos∠APC. Найдем отрезки АС, АР, РС.
4) Из ΔАВС , АС²=2а² , АС=а√2.
Из ΔАВМ , АМ²=2а² , АМ=а√2.
Из ΔАМD , DM²=2а²+a² , DM²=3a² ,DM=a√3 .
ΔADM подобен ΔPDA по 2-м углам : ∠D-общий , ∠МАD=∠APD=90°, значит сходственные стороны пропорциональны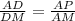
,
АР=(AD*AM):DM=(а*а√2) :a√3=a*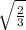
.
ΔADP=ΔCDP как прямоугольные по катету и гипотенузе⇒РС=a*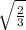
.
4) "Закидываем " найденные значения в АС²=АР²+РС²-2*АР*РС*cos∠APC.
(а√2)²=2*(a*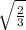
)²-2*(a*
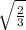) cos∠APC ,
2a²=2a² *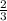
-2a² * 
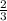*cos∠APC ,
1=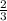
(1 - cos∠APC) , cos∠APC= -0,5 ,∠APC=120° .