Визначте, яка з наведених рівностей випливає з умови, що у різносторонньому трикутнику ABC відрізок CD є бісектрисою

Отрезок ЕС равен 1 см.

Объяснение:

Требуется найти отрезок ОС.

Дано: ΔАВС - равнобедренный;

∠А = 75°;

CD ⊥ АВ; DE ⊥ BC;

ВЕ = 3 см.

Найти: ЕС.

1. Рассмотрим ΔΔАВС - равнобедренный;

Углы при основании равнобедренного треугольника равны.

⇒ ∠А = ∠С = 75°

Сумма углов треугольника равна 180°.

⇒ ∠В = 180° - (75° + 75°) = 30°

2. Рассмотрим ΔDBE - прямоугольный.

∠В = 30°

Катет, лежащий против угла в 30°, равен половине гипотенузы.

Пусть DE = x см, тогда DB = 2x см.

По теореме Пифагора:

BD² = DE² + BE²

4x² = x² + 9

3x² = 9

x² = 3

x = √3

DE = √3 см

3. Рассмотрим ΔАDC - прямоугольный.

Сумма острых углов прямоугольного треугольника равна 90°.

⇒ ∠1 = 90° - ∠А = 90° - 75° = 15°

4. Рассмотрим ΔEDC - прямоугольный.

∠2 = ∠С - ∠1 = 75° - 15° = 60°

∠3 = 90° - ∠2 = 90° - 60° = 30°

Пусть ЕС = у см, тогда DC = 2у см (катет, лежащий против угла 30°)

По теореме Пифагора:

DC² = DE² + EC²

4y² = 3 + y²

3y² = 3

y² = 1

y = 1

Отрезок ЕС равен 1 см.

a = 5 см,

b = 4 см,

c = 7 см.

Найти R.

Запишем теорему синусов:

числитель и знаменатель дроби слева последнего равенства домножим на (b·c).

С учётом того, что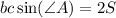 , где S - площадь данного в условии треугольника, имеем

Площадь треугольника можно найти по формуле Герона:

, где

Найдем, сначала, площадь треугольника.

p = (5+4+7)/2 = (9+7)/2 = 16/2 = 8 см.

S = √(8·(8-5)·(8-4)·(8-7)) = √(8·3·4·1) = 4·(√6) см²

Теперь найдем радиус описанной окружности.

R = 5·4·7/(4·4·(√6)) = 5·7/(4·(√6)) = 35·(√6)/(4·6) = 35·(√6)/24 см.

Теперь найдём длину окружности, описанной около данного треугольника.

L = 2πR = 2π·35·(√6)/24 см = π·35·(√6)/12 см.