AC = 18 см, ∠CAD = 20°, ∠BAC = 40°
Т.к. AB ║ CD, то ∠ACD = ∠BAC = 40° (как накрест лежащие)
Сумма углов ΔACD равна 180° ⇒ ∠ADC = 180° - ∠ACD - ∠CAD = 180° - 20° - 40° = 120°
По теореме синусов для ΔACD:
ответ: Стороны параллелограмма равны: см и см
AC = 18 см, ∠CAD = 20°, ∠BAC = 40°
Т.к. AB ║ CD, то ∠ACD = ∠BAC = 40° (как накрест лежащие)
Сумма углов ΔACD равна 180° ⇒ ∠ADC = 180° - ∠ACD - ∠CAD = 180° - 20° - 40° = 120°
По теореме синусов для ΔACD:
ответ: Стороны параллелограмма равны: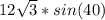 см и
см и 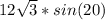 см
см