а = √13 - длина стороны ромба
d = 4 - меньшая диагональ
Поскольку диагонали ромба взаимно перпендикулярны, то найдём вторую диагональ D по теореме Пифагора
D = 2√(a² - (0,5d)²) = 2 · √(13 - 4) = 6
Площадь ромба S = 0.5·d · D = 0.5 · 4 · 6 = 12
Начертили ромб ABCD.
Рассмотрим ΔAOD:
АО=2
AD=√13
OD²=AD²-AO²
OD²=13-4
OD=3
BD=6
Sabcd=×d1×d2
Sabcd= 12
а = √13 - длина стороны ромба
d = 4 - меньшая диагональ
Поскольку диагонали ромба взаимно перпендикулярны, то найдём вторую диагональ D по теореме Пифагора
D = 2√(a² - (0,5d)²) = 2 · √(13 - 4) = 6
Площадь ромба S = 0.5·d · D = 0.5 · 4 · 6 = 12
Начертили ромб ABCD.
Рассмотрим ΔAOD:
АО=2
AD=√13
OD²=AD²-AO²
OD²=13-4
OD=3
BD=6
Sabcd=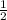 ×d1×d2
×d1×d2
Sabcd= 12