К окружности проведены касательная и секущая, проходящая через центр окружности. Длина касательной в два раза меньше длины секущей. Найдите отношение длины касательной к длине радиуса.
Объяснение:
По условию 2АМ=МС. Пусть радиус окружности r. Нужно найти .
" Если из точки, лежащей вне окружности, проведены касательная и секущая, то квадрат длины касательной равен произведению секущей на ее внешнюю часть: MC2 = MA•MB. "
Одна окружность вписана в прямоугольную трапецию, а вторая касается большей боковой стороны и продолжения оснований.
* * * ABCD трапеция: AD || BC ; ∠BAD =|∠ABC= 90° * * *
а) найдите расстояние между центрами окружностей если большая боковая сторона трапеции равна 17 ; * * * CD =17 * * *
б) Найдите расстояние от вершины одного из прямых углов трапеции до центра второй окружности, если точка касания первой окружности с большей боковой стороной трапеции делит её на отрезки, равные (17-√93)/2 и (17+√93)/2) . * * * CK =(17-√93)/2 ; DK = (17+√93)/2) * * *
ответ: а) 17 , b) 25 .
Объяснение :
a) OO₁ = AD+BC-2r= AD + BC - AB ;
т.к.ABCD описанный четырехугольник , то AD + BC=AB +CD ⇔
К окружности проведены касательная и секущая, проходящая через центр окружности. Длина касательной в два раза меньше длины секущей. Найдите отношение длины касательной к длине радиуса.
Объяснение:
По условию 2АМ=МС. Пусть радиус окружности r. Нужно найти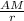 .
.
" Если из точки, лежащей вне окружности, проведены касательная и секущая, то квадрат длины касательной равен произведению секущей на ее внешнюю часть: MC2 = MA•MB. "
АМ²=МВ*МС , но длина отрезка МВ=МС-2r ,
АМ²=( МС-2r)*2АМ |: АМ , МС=2АМ ,
АМ=(2АМ-2r)*2,
3АМ=4r ⇒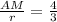 .
.
Одна окружность вписана в прямоугольную трапецию, а вторая касается большей боковой стороны и продолжения оснований.
* * * ABCD трапеция: AD || BC ; ∠BAD =|∠ABC= 90° * * *
а) найдите расстояние между центрами окружностей если большая боковая сторона трапеции равна 17 ; * * * CD =17 * * *
б) Найдите расстояние от вершины одного из прямых углов трапеции до центра второй окружности, если точка касания первой окружности с большей боковой стороной трапеции делит её на отрезки, равные (17-√93)/2 и (17+√93)/2) . * * * CK =(17-√93)/2 ; DK = (17+√93)/2) * * *
ответ: а) 17 , b) 25 .
Объяснение :
a) OO₁ = AD+BC-2r= AD + BC - AB ;
т.к.ABCD описанный четырехугольник , то AD + BC=AB +CD ⇔
AD +BC- AB =CD . Значит OO₁ = 17
б) ∠BCD +∠ADC =180° ⇔ 0,5∠BCD+0,5∠ADC = 90°
⇔ ∠OCD+∠ODC =90° ⇒ ∠COD =90° ;
Из ΔCOD : [ OK ⊥CD ]
OK² =CK*DK=(17-√93)/2*(17+√93)/2) =(17²-93)/4=(289 -93)/4=196/4 =49
r =OK=7 ;
Из ΔBMO₁: BO₁ =√(r² +(r+OO₁)² =√(7² +(7+17)² =√(49+576) =625 =25.