Кротчайшее расстояние от точки С до прямой AB будет лежать на высоте треугольника ABC - CH. Для точки D, соответственно кратчайшим расстоянием до AB будет расстояние DH. Найдём катет прямоугольного треугольника CB обозначив его за x: x^2 + x^2 = 16^2. x = . Далее в прямоугольном треугольнике СHB найдём СH: . Далее найдём в прямоугольном (по условию) треугольнике CDH расстояние DH:
Для решения данной задачи, давайте разделим ее на несколько шагов:
Шаг 1: Найдем длину отрезка сс'.
Для этого воспользуемся свойством прямоугольного треугольника: гипотенуза в квадрате равна сумме квадратов катетов.
Имеем:
ав = 16 - длина катета,
ас = 16 - длина второго катета,
Зная, что угол с в треугольнике авс равен 90°, можем применить теорему Пифагора:
16^2 = (ав)^2 + (ас)^2
256 = (ав)^2 + (16 - ав)^2
256 = ав^2 + 256 - 32ав + ав^2
ав^2 - 32ав = 0
ав (ав - 32) = 0
Значит, ав = 0 или ав = 32.
Учитывая, что ав - это длина стороны треугольника, ав не может равняться 0.
Следовательно, ав = 32.
Шаг 2: Найдем длину отрезка с'д.
Из условия задачи известно, что отрезок сд перпендикулярен к плоскости авс и его длина равна 6.
Шаг 3: Найдем длину отрезка дd'.
Чтобы найти расстояние от точки d до прямой ав, мы можем найти длину отрезка дд', где точка d' - это точка пересечения перпендикуляра с прямой ав.
Заметим, что треугольник авс и треугольник авс' являются подобными.
Это означает, что их соответствующие стороны пропорциональны.
Используем это свойство для нахождения длины отрезка дд':
ав / авс = авс' / авс
32 / 16 = авс' / 16
авс' = 32
Таким образом, длина отрезка дд' также равна 32.
Шаг 4: Найдем расстояние от точки d до прямой ав.
Расстояние от точки d до прямой ав равно длине отрезка дд' минус длина отрезка сд.
32 - 6 = 26
Ответ: Расстояние от точки d до прямой ав равно 26.
Попытаюсь решить на уровне 9 класса.
Кротчайшее расстояние от точки С до прямой AB будет лежать на высоте треугольника ABC - CH. Для точки D, соответственно кратчайшим расстоянием до AB будет расстояние DH. Найдём катет прямоугольного треугольника CB обозначив его за x: x^2 + x^2 = 16^2. x =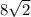
. Далее в прямоугольном треугольнике СHB найдём СH: 
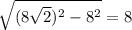. Далее найдём в прямоугольном (по условию) треугольнике CDH расстояние DH: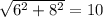 
ответ: 10
Шаг 1: Найдем длину отрезка сс'.
Для этого воспользуемся свойством прямоугольного треугольника: гипотенуза в квадрате равна сумме квадратов катетов.
Имеем:
ав = 16 - длина катета,
ас = 16 - длина второго катета,
Зная, что угол с в треугольнике авс равен 90°, можем применить теорему Пифагора:
16^2 = (ав)^2 + (ас)^2
256 = (ав)^2 + (16 - ав)^2
256 = ав^2 + 256 - 32ав + ав^2
ав^2 - 32ав = 0
ав (ав - 32) = 0
Значит, ав = 0 или ав = 32.
Учитывая, что ав - это длина стороны треугольника, ав не может равняться 0.
Следовательно, ав = 32.
Шаг 2: Найдем длину отрезка с'д.
Из условия задачи известно, что отрезок сд перпендикулярен к плоскости авс и его длина равна 6.
Шаг 3: Найдем длину отрезка дd'.
Чтобы найти расстояние от точки d до прямой ав, мы можем найти длину отрезка дд', где точка d' - это точка пересечения перпендикуляра с прямой ав.
Заметим, что треугольник авс и треугольник авс' являются подобными.
Это означает, что их соответствующие стороны пропорциональны.
Используем это свойство для нахождения длины отрезка дд':
ав / авс = авс' / авс
32 / 16 = авс' / 16
авс' = 32
Таким образом, длина отрезка дд' также равна 32.
Шаг 4: Найдем расстояние от точки d до прямой ав.
Расстояние от точки d до прямой ав равно длине отрезка дд' минус длина отрезка сд.
32 - 6 = 26
Ответ: Расстояние от точки d до прямой ав равно 26.