Выберите правильный вариант ответа, докажите почему вы выбрали именно его:

треугольник является остроугольным, если
а) среди его углов нет тупого
б) каждый его угол меньше прямого
в) среди его углов нет прямого
г) каждый его угол меньше тупого
​

Объяснение:

Найдём критические точки (это те значения в которых производная функции равна нулю или не имеет значений (к примеру 1/x, при x=0 функция не имеет значения), они называются точками разрыва).

Сразу видно что у функции нет точек разрыва (то есть она определена на всей числовой прямой), поэтому просто приравняем производную функции к нулю:

[Производная степенной функции: ]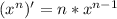

Произведение равно нулю, когда хотя бы один из множителей равен нулю:

3x=0       или      x+2=0

x=0       или      x=-2

Итого у нас 2 точки экстремума.

Теперь посмотрим как ведёт себя производная функции между ними. Там, где производная принимает положительные значения, сама функция возрастает, там где отрицательные - убывает.

(Рисунок)

Как видно из рисунка, функция возрастает на промежутке (-∞;-2)U(0;+∞) и убывает на (-2;0)

Точки экстремума:

-6 ; 0

Монотонность функции:

функция возрастает на промежутке (-∞;-2)U(0;+∞)

функция убывает на промежутке (-2;0)

ответ:Треугольник RFE равен треугольнику ЕFS

Оба эти треугольника прямоугольные,по четвёртому признаку равенства прямоугольных треугольников-по гипотенузе и по острому углу,они равны

EF-общая сторона,она же гипотенуза

<SEF=<REF ,по условию задачи

Номер 2

Треугольник АDE равен треугольнику FMB

Данные треугольники прямоугольные,они равны по 4 признаку равенства прямоугольных треугольников -по гипотенузе и острому углу

AD=FB по условию задачи

<А=<В, т к треугольник АСВ равнобедренный,а углы при основании равнобедренного треугольника равны между собой

А равнобедренный,т к

АD=FB;DC=CF; по условию задачи

Объяснение: