Т.к. треугольник ABC равнобедренный, тогда угол BAC = углу BCA = 30'. BO-является высотой, биссектрисой и медианой и радиусом.
Угол OBC = углу OBA =60' Центр описанной окружности треугольника находится на пересечении серединных перпендикуляров. Следовательно, CN=NB=BM=MA=2,5.
Рассмотрим треугольник NOB: NO перпендикулярна BC. Угол NBO=60', тогда угол BON=30'. А в прямоугольном треугольнике катет, лежащий против угла в 30', равен половине гипотенузы. Значит, BO=5. BO является радиусом окружности, тогда d=2r или d=2*5=10.
Решение:
Т.к. треугольник ABC равнобедренный, тогда угол BAC = углу BCA = 30'.
BO-является высотой, биссектрисой и медианой и радиусом.
Угол OBC = углу OBA =60' Центр описанной окружности треугольника находится на пересечении серединных перпендикуляров. Следовательно, CN=NB=BM=MA=2,5.
Рассмотрим треугольник NOB: NO перпендикулярна BC.
Угол NBO=60', тогда угол BON=30'. А в прямоугольном треугольнике катет, лежащий против угла в 30', равен половине гипотенузы. Значит, BO=5.
BO является радиусом окружности, тогда d=2r или d=2*5=10.
ответ: d=10.
Первая часть задачи решена Пользователем 5SashaRyskin5.
Добавлен рисунок и нахождение двух других высот.
P=64, cos A=cos C=0,28. BD-высота. Найди: BD.
1) Cos A=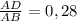
AC+2AB=64, AC=2AD, 2AD+2AB=64, 2*(AD+AB)=64, AD+AB=32.
AB=32 - AD.
Пусть х=AD, тогда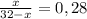
Решаем уравнение.
224 - 7x = 25x
х=7. AD=7, АB=32-7=25.
Рассмотри треугольник ABD.
BD=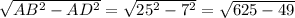 = 24
= 24
ответ: BD=24 см.
2) AC = 2AD = 7 · 2 = 14 см
Sabc = 1/2 · AC · BD = 1/2 · AB · CH
CH = AC · BD / AB = 14 · 24 / 25 = 13,44 см
АК = СН = 13,44 см как высоты, проведенные к равным сторонам.