Высота правильной усеченной прямоугольной пирамиды - 12 см, разница краев основания - 10 см, площадь всей поверхности - 512 см. Вычислите длины краев основания пирамиды.

Показать ответ

Ответ:

FireFox2017

01.04.2022 14:57

Дано
сторона основания a=√3
боковое ребро b = 3
Найти
площадь сечения,проведенного через сторону основания и середину противоположного бокового ребра пирамиды
Решение
Линия ,соединяющая вершину стороны основания с серединой противоположного бокового ребра пирамиды - это медиана боковой грани - m
Искомое сечение состоит из 2-х медиан и стороны основания. Это равнобедренный треугольник.
Найдем медиану по известной ф-ле
m = 1/2 √ ( 2(a^2+b^2) - b^2 ) = 1/2 √ ( 2a^2+b^2) =1/2 √ (2(√3)^2+3^2) =1/2 √15
полупериметр сечения p=P/2=(m+m+a)/2=m+a/2 =1/2 √15 +1/2 √3 =1/2 (√15 +√3)
площадь сечения по ф-ле Герона
S = √ ( p(p-a)(p-m)(p-m) )=(p-m)√ ( p(p-a) )=
= (1/2 (√15 +√3) - 1/2 √15)√ ( 1/2 (√15 +√3) (1/2 (√15 +√3) -√3) )=
= 1/2 √3 √ ( 1/2 (√15 +√3) * 1/2 (√15 -√3) )= 1/4 √3 √(√15^2 -√3^2)=
=1/4 √3 √12=1/4 √(3*12) =1/4 *6 =3/2 (или=1.5)
ответ 3/2 (или=1.5)

0,0(0 оценок)

Ответ:

Kuznetsova8903

20.07.2020 07:53

Нет

Объяснение:

Рассмотрим белый (незаполненный) прямоугольный треугольник.

Мы знаем длину большего катета (=ребру куба=a) и прилежащий угол = 30°. Следовательно, второй острый угол =180-90-30=60°.

Найдём длину второго катета b:

гипотенуза с= $\frac{a}{sin60}=\frac{2a}{\sqrt{3} }$ ,

$b=c*cos60=\frac{2a}{\sqrt{3} }*\frac{1}{2}=\frac{a}{\sqrt{3} }.$

Определим площадь треугольника $S=\frac{1}{2}ab=\frac{a}{2}*\frac{a}{\sqrt{3} }=\frac{a^{2} }{2\sqrt{3} }$ .

Значит, объём, который останется незаполненным, равен объёму призмы с рассматриваемым нами треугольником в основании:

V(незаполненный)=Vпризмы=SΔ×a=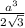 $\frac{a^{3} }{2\sqrt{3} }$ .

Объём максимально доступный нам для наполнения логично равен Vmax=V(куба)-V(незаполненный)= $a^{3}-\frac{a^{3}}{2\sqrt{3}}=\frac{a^{3}(2\sqrt{3}-1)}{2\sqrt{3}}$ .

Наконец, найдём отношение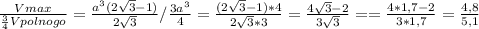 $\frac{Vmax}{\frac{3}{4}Vpolnogo }=\frac{a^{3}(2\sqrt{3}-1)}{2\sqrt{3}}/\frac{3a^{3}}{4}=\frac{(2\sqrt{3}-1)*4 }{2\sqrt{3}*3}=\frac{4\sqrt{3}-2}{3\sqrt{3}}==\frac{4*1,7-2}{3*1,7}=\frac{4,8}{5,1}$ <1, следовательно Vmax< 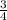$\frac{3}{4}$ Vполного, т.е. наполнить сосуд водой на три четверти не получится.