З точки Е до площини α проведено перпендикуляр EL і похилу EN . Знайдіть проекцію похилої EN на площину α і довжину перпендикуляра EL , якщо EN = 8 √3 см, а кут ENL= 30
Теорема . три высоты любого треугольника пересекаются в одной точке. доказательство: пусть abc - данный треугольник . пусть прямые, содержащие высоты ap и bq треугольника abc пересекаются в точке o. проведем через точку a прямую, параллельную отрезку bc, через точку b прямую, параллельную отрезку ac, а через точку c - прямую, параллельную отрезку ab. все эти прямые попарно пересекаются. пусть точка пересечения прямых, параллельных сторонам ac и bc - точка m, точка пересечения прямых, параллельных сторонам ab и bc - точка l, а прямых, параллельным ab и ac - точка k. точки klm не лежат на одной прямой, (иначе бы прямая ml совпадала бы с прямой mk, а значит, прямая bc была бы параллельна прямой ac, или совпадала бы с ней, то есть точки a, b и c лежали бы на одной прямой, что противоречит определению треугольника) . итак, точки k, l, m составляют треугольник. ma параллельно bc, и mb параллельно ac по построению. а значит, четырёхугольник macb - параллелограмм. следовательно, ma = bc, mb = ac. аналогично al = bc = ma, bk = ac = mb, kc = ab = cl. значит, ap и bq - серединные перпендикуляры к сторонам треугольника klm. они пересекаются в точке o, а значит, co - тоже срединный перпендикуляр. co перпендикулярно kl, kl параллельно ab, а значит co перпендикулярно ab. пусть r - точка пересечения ab и cq. тогда cr перпендикулярно ab, то есть cr - это высота треугольника abc. точка o принадлежит всем прямым, содержащим высоты треугольника abc. значит, прямые, содержащие высоты этого треугольника пересекаются в одной точке. что и требовалось доказать.
Чертежи смотрите во вложении.
✧Задание №1.✧
В прямоугольном равнобедренном треугольнике гипотенуза равна 12 см. Найти катеты этого треугольника.
Дано :
ΔАВС - равнобедренный и прямоугольный (∠В = 90°, АВ = СВ).
АС = 12 см.
Найти :
АВ = ?
СВ = ?
В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы (теорема Пифагора).Пусть АВ = СВ = х. Тогда АВ² + СВ² = АС²
х² + х² = 12²
2х² = 144
х² = 72
х₁ =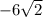 - не удовлетворяет условию задачи, так как длины отрезков не могут выражаться отрицательными числами.
- не удовлетворяет условию задачи, так как длины отрезков не могут выражаться отрицательными числами.
х₂ =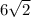 - подходит.
- подходит.
Тогда АВ = СВ = х =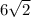 см.
см.
✧Задание №2.✧
Найти меньшую диагональ ромба, если его сторона равна 13 см, а большая диагональ ромба равна 24 см.
Дано :
Четырёхугольник ABCD - ромб.
ВС = 13 см, АС = 24 см.
Найти :
BD = ?
В ромбе диагонали точкой пересечения делятся пополам и взаимно перпендикулярны.Следовательно, АС⊥BD, ВО =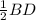 , CO =
, CO = 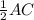 =
= 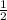 *24 см = 12 см.
*24 см = 12 см.
Рассмотрим ΔВОС - прямоугольный (∠ВОС = 90°).
По теореме Пифагора -
ВО² + СО² = ВС²
ВО² = ВС² - СО² = 13² - 12² = 169 - 144 = 25 ⇒ ВО =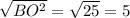 см.
см.
Тогда BD = 2*BO = 2*5 см = 10 см.
10 см.