Задача 2. Угол АCВ с величиной 50° вписана окружность, которая касается сторон
угла в точках A и B, точка O — центр окружности. Найдите угол AOB. ответ дайте
в градусах.
Задание 3 Из центра окружности О к хорде MN, равной 40 см, проведен
перпендикуляр ОС. Найдите длину перпендикуляра, если < ОMN = 450
.
Задача No4. Найдите площадь квадрата, описанного около окружности радиуса 6.
1.Пусть одна сторона равна х, тогда другая 6х. У параллелограмма противолежащие стороны равны. Сумма сторон равна 84. Тогда составим уравнение
х+х+6х+6х=84
14х=84
х=84:14
х=6
Тогда 6х=6×6=36
Проверка: 6+6+36+36=84
ответ: 6; 6; 36; 36
2.В прямоугольнике противоположные стороны равны. Значит ВС=АD=18см
BD и АС являются диагоналями прямоугольника ABCD.
Диагонали в прямоугольнике равны, т.е BD=АС=22см
О-точка пересечения диагоналей, которая делит их пополам. Значит ОD=ОА=ОВ=ОС=1/2 BD=11см
Рboc=ОB+ОC+ВC
Рboc=11+11+18=40см
3.диагонали ромба являются биссектрисами его углов (то есть делят их пополам);
сумма соседних углов ромба равна 180°;
противоположные углы ромба равны
4.Диагональ АС делит параллелограмм на 2 подобных треугольника. Углы NAB=PCD, угол ABN=CDP и следовательно углы BNA= СPD, отсюда следует что прямоугольники ABN и CDP также подобны. Следовательно прямые BN и PD равны между собой. Что и требовалось доказать
5.Примем коэффициент отношения AF:FD=a. Тогда AF=a, FD=5a. Их сумма 6а=18 см, ⇒ а=18:6=3 см. Отрезок АF=3 см, отрезок FD=5•3=15 см АВСD - параллелограмм. ВС║AD, CF – секущая. ∠ВСF=∠СFD как накрестлежащие. Но ∠FCD=∠BCF (СF – биссектриса) ⇒ ∠CFD=∠FCD . Углы при основании FC треугольника FDC равны, следовательно, он равнобедренный и CD=FD=15 см ( свойство). Запомним: Биссектриса угла параллелограмма отсекает от него равнобедренный треугольник. Противоположные стороны параллелограмма равны, ⇒ АВ=CD=15 см. Периметр =сумма всех сторон АВСD. Р=2•(18+15)=66 см
Нехай є трикутна піраміда, сторони основи якої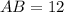 см,
см, 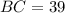 см,
см, 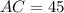 см. Якщо всі бічні грані піраміди нахилені до основи під кутом
см. Якщо всі бічні грані піраміди нахилені до основи під кутом 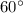 , то висота
, то висота 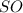 піраміди лежить у центрі
піраміди лежить у центрі 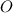 вписаного кола, де
вписаного кола, де 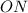 ,
, 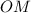 та
та 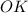 — радіуси цього кола.
— радіуси цього кола.
Треба знайти площу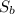 бічної поверхні піраміди. Для того щоб її знайти, треба визначити площу кожної бічної грані.
бічної поверхні піраміди. Для того щоб її знайти, треба визначити площу кожної бічної грані.
Знайдемо площу основи за формулою Герона:
Знайдемо радіус вписаного кола:
Отже,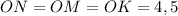 см.
см.
Розглянемо прямокутний трикутник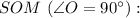
Розглянемо трикутник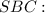
Розглянемо трикутник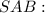
Розглянемо трикутник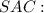
Отже, площею бічної поверхні заданої піраміди буде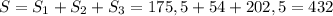 см².
см².
Відповідь: 432 см².