ЗАДАЧИ НА ПОСТРОЕНИЕ РЕШИТЬ КАК НАДО, С РИСУНКОМ, ДАНО И Т.Д. И В БЛИЖАЙШЕЕ ВРЕМЯ...
1) Построить прямоугольный треугольник по двум данным катетам. 2) Для заданной окружности постройте точку, которая является центром. 3) Постройте окружность данного радиуса, проходящую через 2 данные точки(можно использовать равнобедренный треугольник)
1) дано угол В=30 градусов ВА=4 см
решение
проведем АС перпендикуляр к прямой а угол ВСА=90 градусов
получим прямоугольный треугольник АВС
пусть АС=х тогда по свойству что против угла в 30 градусов лежит катет равный половине гипотинузы х=ВА\2
значит АС= 2 см ответ 2 см
2) дано: треугольник АВС равнобедренный (так как угли при основании равны) ВС=14см
проведем АР
т.к. АВС равнобедренный то АР высота медиана биссектриса
значит ВР=СР=14\2=7см
треугольник арс прямоугольный и равнобедренный т.к. угол рас =180-90-45=45 градусов
значит ар=7см
3) тут не дано ни одной величины
это треугольник прямоугольный т.к. 180-30-60=90
значит катет лежащий против угла в 30 градсов равен половине гипотинузы следовательно ас=х тогда вс=2х
тогда ва^2=4х^2-x^2
ва=х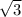
если провести высоты ар то получим новый прямоугольный треугольник вра в котором ар=(х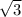 )\2
)\2
Объяснение:
Выберите верные утверждения: *
Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого, то такие треугольники равны.
Если две стороны одного прямоугольного треугольника соответственно равны двум сторонам другого, то такие треугольники равны.
Если катет и острый угол одного прямоугольного треугольника соответственно равны катету и острому углу другого, то такие треугольники равны.
Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого, то такие треугольники равны.
Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого, то такие треугольники равны.