задание: катеты прямоугольного треугольника равны 7см и 24см. Вычислите синус, косинус, тангенс и котангенс наименьшего угла треугольника.
2задание: найдите значения тригонометрических функций острого угла А, если
3задание: определите, могут ли синус и косинус одного угла соответственно быть равными:
4задание: определите, могут ли тангенс и котангенс одного угла соответственно быть равными: 1)0,4 и 2,5. 2)1,1 и 0,9.
5 задание: упрастите выражение:
6задание: катеты прямоугольного треугольника равны 8см и 15см. Найдите значения тригонометрических функций наименьшего угла треугольника.
7задание: упростите вырождение:

​

Нехай задана правильна трикутна призма, бічні грані якої є квадратами, а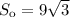 см² — площа основи цієї призми.

Основа призми є правильним (рівностороннім) трикутником зі строною см. Знайдемо цю сторону, скориставшись площею рівностороннього трикутника: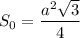

Отже,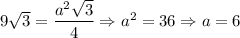 см.

Через те що бічні грані є квадратами, тоді ребра призми дорівнюють 6 см (за властивістю квадрата) — ребра правильної призми є висотою призми.

Об'єм правильної трикутної призми можна розрахувати за формулою

, де см — висота призми.

Знайдено значення шуканої величини:

см³

Відповідь: А)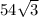 см³

Объяснение:

№1

Так как АВС-прямоугольный, то сумма острых углов 90°=>угол В =90 - угол А =90 - 37=53°

№2

Так как АС=АВ =>угол А =углу В

Так как АВС - прямоугольный, то угол А=углу В=(180-90):2=45°

№3

А=С =45°(так же как и во 2 задаче)

Так как АВС-равнобедренный, то BD и высота (по рисунку ) и биссектриса =>так как В =90°,то АBD=DBC=45 °(можно было ещё по сумме углов треугольника BDC доказать что DBC=45°)

Угол С=45 (по доказ.),угол DBC=45°=>ВDC - равнобедренный (так как углы по. Основании равны, где основание ВС)

Что и требовалось доказать.

№4

Рассмотрим DBC, по сумме острых углов прямоугольного треугольника (=90°),угол DCB=90-70=20°

По рисунку CD-биссектриса=>угол DCB=ACD=20°

Угол ADC и CDB смежные =>их сумма 180°=>ADC=180-70=110°

Рассмотрим треугольник ADC

Так как сумма углов треугольника 180°,то угол CAD=180-(20+110)=180°-130°=50°