Рассмотрим ΔABC - равнобедренный; AB=BC=25 см;
BD - медиана ⇒ AD=DC=14:2=7 см
Т.к. ΔABC - равнобедренный, то BD - является и высотой, и биссектрисой еще.
Рассмотрим ΔABD - прямоугольной; ∠D - прямой, AB=25см; AD=7 см
по т. Пифагора найдем BD
BD² = AB² - AD²
BD² = 25² - 7²
BD = 24 cм
Рассмотрим еще раз ΔABC:
по свойству медианы OD=1/3 * BD = 1/3 * 24 = 24 : 3 = 8 см
Рассмотрим ΔCOD - прямоугольный; ∠D - прямой; DC=7 см; OD=8 см
по т.Пифагора найдем OC
OC² = OD² + DC²
OC² = 8² + 7²
OC = см
по свойству медианы см
по свойству равнобедренного треугольника CH=AK= см
ответ: 24 см; см; см
Рассмотрим ΔABC - равнобедренный; AB=BC=25 см;
BD - медиана ⇒ AD=DC=14:2=7 см
Т.к. ΔABC - равнобедренный, то BD - является и высотой, и биссектрисой еще.
Рассмотрим ΔABD - прямоугольной; ∠D - прямой, AB=25см; AD=7 см
по т. Пифагора найдем BD
BD² = AB² - AD²
BD² = 25² - 7²
BD = 24 cм
Рассмотрим еще раз ΔABC:
по свойству медианы OD=1/3 * BD = 1/3 * 24 = 24 : 3 = 8 см
Рассмотрим ΔCOD - прямоугольный; ∠D - прямой; DC=7 см; OD=8 см
по т.Пифагора найдем OC
OC² = OD² + DC²
OC² = 8² + 7²
OC =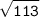 см
см
по свойству медианы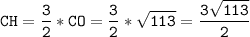 см
см
по свойству равнобедренного треугольника CH=AK=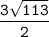 см
см
ответ: 24 см;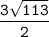 см;
см; 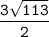 см
см
И тут стоит обратить внимание на боковую сторону. 26 - это 2*13
И вспомнить про существование египетских треугольников:
3,4,5 и 12,5,13.
Значит высота либо 24, либо 10. (так как тут египетский треугольник умноженный на два).
Как же нам вычислить где серединка основания, а где высота?
Через площадь.
С одной стороны площадь =
Если высота 24, то основание 2*10 = 20
Площадь равна:
Однако так же площадь можно посчитать по формуле Герона
Если основание равно 20, то полупериметр будет равен:
Если основание равно 48, то полупериметр будет равен:
Мда, не расставление площадей. К сожалению, я не могу точно определить именно высоту. Надеюсь, хоть чем-то со сторонами.