Знайдіть геометричне місце точок віддалених від даної точки на відстань 5 см
​

В данной задаче может быть два случая:

Как мы знаем, в равнобедренном треугольнике боковые стороны равны.

Значит, у нас есть два случая, если боковая сторона равняется 6 или 8.

1) Если боковые стороны равны по 6 см. Значит, основание равно 8 см. Периметр равнобедренного треугольника равен произведение двух боковых сторон плюс основание треугольника. Найдем периметр треугольника в первом случае:

6 · 2 + 8 = 20 см.

2) Если боковые стороны равны по 8 см. Значит, основание равно 6 см.

Найдем периметр:

8 · 2 + 6 = 22 см.

ответ: Первый случай периметр равен 20 см; Второй случай периметр равен 22 см.

Чертежи смотрите во вложении.

✧Задание №1.✧

В прямоугольном равнобедренном треугольнике гипотенуза равна 12 см. Найти катеты этого треугольника.

Дано :

ΔАВС - равнобедренный и прямоугольный (∠В = 90°, АВ = СВ).

АС = 12 см.

Найти :

АВ = ?

СВ = ?

В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы (теорема Пифагора).

Пусть АВ = СВ = х. Тогда АВ² + СВ² = АС²

х² + х² = 12²

2х² = 144

х² = 72

х₁ =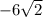 - не удовлетворяет условию задачи, так как длины отрезков не могут выражаться отрицательными числами.

х₂ =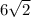 - подходит.

Тогда АВ = СВ = х =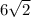 см.

см, см.

✧Задание №2.✧

Найти меньшую диагональ ромба, если его сторона равна 13 см, а большая диагональ ромба равна 24 см.

Дано :

Четырёхугольник ABCD - ромб.

ВС = 13 см, АС = 24 см.

Найти :

BD = ?

В ромбе диагонали точкой пересечения делятся пополам и взаимно перпендикулярны.

Следовательно, АС⊥BD, ВО =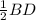 , CO = 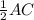= 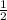*24 см = 12 см.

Рассмотрим ΔВОС - прямоугольный (∠ВОС = 90°).

По теореме Пифагора -

ВО² + СО² = ВС²

ВО² = ВС² - СО² = 13² - 12² = 169 - 144 = 25 ⇒ ВО =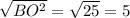 см.

Тогда BD = 2*BO = 2*5 см = 10 см.

10 см.