нам сейчас известна только одна диагональ АС =4(ОС*2), а чтобы найти площадь нужно знать две(диагонали). через теорему пифагора мы найдем вторую диаглналь. с^2=a^2+b^2, b^2=c^2-a^2, b^2=c^2(гипотенуза, в нашем случае это ВС равное 5)-a^2(это ОС равное 2) то есть в^2= 25(это 5 в квадрате) - 4(2 в квадрете) = 21(так и записывай в= корень из 21), вторая диагональ= 2*= корень(4*21)=корень(84). теперь чтобы найти площадь нужно (д1*д2)/2. получается (4*корень(84))/2. запишешь в форме дроби, ото 4 и 2 можно сократить, останется 2
Если трапецию можно вписать в окружность, то она равнобедренная. <CAD=<BCA (как внутренние накрест лежащие при параллельных АВ и CD и секущей АС. Значит и <ВАС=30° (АС - биссектриса) и треугольник АВС равнобедренный. Тогда его высота ВН - это и медиана. Значит ВН - это часть радиуса ВО, так как радиус, перпендикулярный хорде, делит ее пополам. Угол АВС этого треугольника равен 120°. Это вписанный угол, опирающийся на дугу АDC. Значит градусная мера дуги АDC в два раза больше и равна 240°. Тогда градусная мера дуги АВС равна АВС=360°-240°=120°. На эту дугу опирается центральный угол АОС, соответственно равный 120°. Итак, мы имеем четырехугольник АВСО, являющийся ромбом, и точка О лежит на стороне АD нашей трапеции. Следоательно АВ=ВС=АО=ОD=ОС=СD=R=4см. Проведем высоту трапеции СК. В равностороннем треугольнике ОСD высота СК равна (√3/2)*а, где а=4см. СК=2√3см. Площадь трапеции S=(BC+AD)*CК/2=12√3см². ответ: S=12√3см².
тут площадь ромба находится через диагонали.
Объяснение:
нам сейчас известна только одна диагональ АС =4(ОС*2), а чтобы найти площадь нужно знать две(диагонали). через теорему пифагора мы найдем вторую диаглналь. с^2=a^2+b^2, b^2=c^2-a^2, b^2=c^2(гипотенуза, в нашем случае это ВС равное 5)-a^2(это ОС равное 2) то есть в^2= 25(это 5 в квадрате) - 4(2 в квадрете) = 21(так и записывай в= корень из 21), вторая диагональ= 2*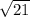
= корень(4*21)=корень(84). теперь чтобы найти площадь нужно (д1*д2)/2. получается (4*корень(84))/2. запишешь в форме дроби, ото 4 и 2 можно сократить, останется 2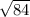
<CAD=<BCA (как внутренние накрест лежащие при параллельных АВ и CD и секущей АС. Значит и <ВАС=30° (АС - биссектриса) и треугольник АВС равнобедренный. Тогда его высота ВН - это и медиана. Значит ВН - это часть радиуса ВО, так как радиус, перпендикулярный хорде, делит ее пополам. Угол АВС этого треугольника равен 120°. Это вписанный угол, опирающийся на дугу АDC. Значит градусная мера дуги АDC в два раза больше и равна 240°. Тогда градусная мера дуги АВС равна АВС=360°-240°=120°.
На эту дугу опирается центральный угол АОС, соответственно равный 120°. Итак, мы имеем четырехугольник АВСО, являющийся ромбом, и
точка О лежит на стороне АD нашей трапеции. Следоательно
АВ=ВС=АО=ОD=ОС=СD=R=4см. Проведем высоту трапеции СК.
В равностороннем треугольнике ОСD высота СК равна (√3/2)*а, где а=4см. СК=2√3см.
Площадь трапеции S=(BC+AD)*CК/2=12√3см².
ответ: S=12√3см².