21см и 14см
Объяснение:
Чертёж не требуется.
Площадь прямоугольника: S=ab
Периметр прямоугольника: Р=2(a+b)
Известно, что Р=70, S=294
Подставим в формулы:
ab=294 (1)
2(a+b)=70, разделим на 2
a+b=35 (2)
Получили систему уравнений (1) и (2)
Выразим а из второго уравнения. а=35-b
Подставим а в первое уравнение:
(35-b)b=294
-b²+35b-294=0, разделим на - 1, применим теорему виета. Хочу заметить, что применить её лучше, чем дискриминант, при решении таких задач, так как мы получим два числа, оба из них являются значениями сторон. Условно b1=a, b2=b
b²-35b+294=0
b1+b2=35
b1b2=294
b1=21=a, b2=14=b
Значит длины сторон составляют 21см и 14см
Відповідь:
Пояснення:
Дано: коло O; коло O1; OB = 5; O1B1 = 3; B∈AB; B1∈AB; AB1 = 4
Знайти: OO1
Розв'язання:
Розглянемо ΔAOB і ΔAO1B1.
∠A - спільний; OB⊥AB, O1B1⊥AB (за властивістю дотичної та радіуса, проведеного в точку дотику). Отже ΔAOB подібний ΔAO1B1 (за двома кутами).
В ΔAO1B1 за теоремою Піфагора знайдемо гіпотенузу AO1
AO1^2 = AB1^2 + O1B1^2
AO1^2 = 4^2 + 3^2 = 16 + 9 = 25
AO1 = = 5
У подібних трикутниках відповідні сторони пропорційні:
OB/O1B1 = AO/AO1
5/3 = AO/5
AO = 5*5/3
AO = 25/3
OO1 = AO - AO1
OO1 = 25/3 - 5 = 10/3
OO1 ≈ 3,3
21см и 14см
Объяснение:
Чертёж не требуется.
Площадь прямоугольника: S=ab
Периметр прямоугольника: Р=2(a+b)
Известно, что Р=70, S=294
Подставим в формулы:
ab=294 (1)
2(a+b)=70, разделим на 2
a+b=35 (2)
Получили систему уравнений (1) и (2)
Выразим а из второго уравнения. а=35-b
Подставим а в первое уравнение:
(35-b)b=294
-b²+35b-294=0, разделим на - 1, применим теорему виета. Хочу заметить, что применить её лучше, чем дискриминант, при решении таких задач, так как мы получим два числа, оба из них являются значениями сторон. Условно b1=a, b2=b
b²-35b+294=0
b1+b2=35
b1b2=294
b1=21=a, b2=14=b
Значит длины сторон составляют 21см и 14см
Відповідь:
Пояснення:
Дано: коло O; коло O1; OB = 5; O1B1 = 3; B∈AB; B1∈AB; AB1 = 4
Знайти: OO1
Розв'язання:
Розглянемо ΔAOB і ΔAO1B1.
∠A - спільний; OB⊥AB, O1B1⊥AB (за властивістю дотичної та радіуса, проведеного в точку дотику). Отже ΔAOB подібний ΔAO1B1 (за двома кутами).
В ΔAO1B1 за теоремою Піфагора знайдемо гіпотенузу AO1
AO1^2 = AB1^2 + O1B1^2
AO1^2 = 4^2 + 3^2 = 16 + 9 = 25
AO1 =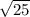 = 5
= 5
У подібних трикутниках відповідні сторони пропорційні:
OB/O1B1 = AO/AO1
5/3 = AO/5
AO = 5*5/3
AO = 25/3
OO1 = AO - AO1
OO1 = 25/3 - 5 = 10/3
OO1 ≈ 3,3