Боковые стороны, значит, равны по 4 см, т.к. равны у равнобедренного треугольника, и синус 120 градусов равен синусу 60 градусов, равен √3/2, тогда площадь равна половине произведения боковых сторон на синус угла между ними.
(4*4*√3/2)/2=4√3/см²/, найдем теперь по теореме косинусов основание равнобедренного треугольника, учитывая , что косинус 120 град. равен -1/2, основание равно
Решение : так как боковые рёбра образуют с высотой пирамиды равные углы, значит, они образуют равные углы с основанием пирамиды (острые углы прямоугольных треугольников, равных по общему катету и острому углу). ⇒ Высота опускается в центр окружности, описанной около основания пирамиды. Основание пирамиды - прямоугольный треугольник, центр описанной окружности лежит на середине гипотенузы. H ∈ AB, AH = BH.
SH⊥(ABC) ⇒ SH⊥AB ⇒ ∠SHA=90°
ΔSAH - прямоугольный равнобедренный, так как ∠SAH=∠ASH=45° ⇒ AH = SH = 4 см ⇒ AB = AH + BH = 8 см; SA = 4√2 см
SA = SB = SC = 4√2 см
ΔABC - прямоугольный. Катет, лежащий против угла 30°, равен половине гипотенузы. BC = AB/2 = 4 см
По теореме Пифагора
AC² = AB² - BC² = 8² - 4² = 48
AC = √48 = 4√3 см
см²
Площадь двух других граней можно найти по формуле Герона
Боковые стороны, значит, равны по 4 см, т.к. равны у равнобедренного треугольника, и синус 120 градусов равен синусу 60 градусов, равен √3/2, тогда площадь равна половине произведения боковых сторон на синус угла между ними.
(4*4*√3/2)/2=4√3/см²/, найдем теперь по теореме косинусов основание равнобедренного треугольника, учитывая , что косинус 120 град. равен -1/2, основание равно
√((4²+4²-2*4*4*(-1/2))=4√3, значит, радиус описанной окружности равен а*в*с/4S=(4*4*4√3)/(4*4√3)=4/см По теореме синусов а/sinα=2*R
R=a/2sinα, найдем угол α при основании и подставим в эту формулу.
Углы при основании равны, поэтому α=(180°-120°)/2=30°
Итак, радиус равен 4/(2sin30°)=4/(2*1/2)=4/cм/
Дано: пирамида SABC, SH⊥(ABC), SH = 4 см,
∠ASH=∠CSH=∠BSH=45°, ∠ACB=90°, ∠BAC=30°
Найти : Sбок
Решение : так как боковые рёбра образуют с высотой пирамиды равные углы, значит, они образуют равные углы с основанием пирамиды (острые углы прямоугольных треугольников, равных по общему катету и острому углу). ⇒ Высота опускается в центр окружности, описанной около основания пирамиды. Основание пирамиды - прямоугольный треугольник, центр описанной окружности лежит на середине гипотенузы. H ∈ AB, AH = BH.
SH⊥(ABC) ⇒ SH⊥AB ⇒ ∠SHA=90°
ΔSAH - прямоугольный равнобедренный, так как ∠SAH=∠ASH=45° ⇒ AH = SH = 4 см ⇒ AB = AH + BH = 8 см; SA = 4√2 см
SA = SB = SC = 4√2 см
ΔABC - прямоугольный. Катет, лежащий против угла 30°, равен половине гипотенузы. BC = AB/2 = 4 см
По теореме Пифагора
AC² = AB² - BC² = 8² - 4² = 48
AC = √48 = 4√3 см
Площадь двух других граней можно найти по формуле Герона
ΔASC,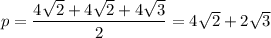
ΔBSC,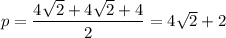
ответ: 4(4 + √15 + √7) см²