1) Найти: AB,AB, , ,A\B,B\A Изобразите диаграммы Эйлера 2)С таблицы истинности проверить справедливость следующего тождества:
3)Упростить логическое выражение:
Описать выполнение каждого задания.

По условию элементы массива могут принимать абсолютно любые значения, т.е. могут быть любыми рациональными числами.

Первый цикл будет вычислять среднее арифметическое положительных элементов. В переменной s будет храниться общая сумма их значений, а в sk - их кол-во.

Далее, после цикла, общая сумма делится на общее кол-во и получается среднее арифметическое. Притом неясно, а что если массив не имеет положительных элементов? Будет неопределенность вида 0/0, непонятно каким образом обработанная программой (и алгоритмом).

Далее считается кол-во элементов, больших среднего значения. И тут опять же, ничего определенного сказать нельзя. В силу произвольности значений элементов массива, это кол-во может быть любым (но не большим n).

А что если среднее значение есть неопределенность 0/0 ? Относительно нее осуществлять операции сравнения... кхм, вообще непредсказуемая операция.

Итого: sk на выходе может быть любым, задача сформулирована убого.

(см. объяснение)

Объяснение:

Число 21 в развернутой форме записи можно представить так:

Из условия задачи следует, что последнее число в системе счисления с основанием n равно 0, т.е. .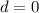

Тогда получим:

Заметим, что n можно вынести за скобки:

Разделим обе части равенства на n:

Получили, что 21 делится на основание системы счисления без остатка.

Учитывая, что n>1, наименьший делитель числа 21 - это 3.

Поэтому минимальное основание системы счисления, при записи числа 21 в которой последним символом будет 0 равно 3.

И действительно .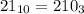

Задача решена!