Даны действительные числа х, у. определить, принадлежит ли точка с координатами х, у заштрихованной части плоскости. на java. есть готовый ответ: но у меня почему-то ничего не происходит, когда я запускаю программу.
Взял 1000 потому что думал, что должно быть меньше. Если бы программа не сработала взял бы либо отрицательные числа, либо больше тысячи (возможно бы пришлось изменить тип данных).
Решение основано на обыкновенном вычислении периода дроби (для дробей, имеющих конечную десятичную запись(например, 1/2=0,5), период вычисляется для формы с нулем в периоде(то есть для 1/2 берется форма 0,5(0))) с деления столбиком.
Замечание: сам алгоритм деления в столбик я писал достаточно давно, и для других программ, поэтому его реализация в данном коде может быть неоптимальной (в плане памяти или кол-ва операций), однако он работает.
Вариант 2: файл 3.cpp
Если немного углубиться в математику, можно найти теорему, по которой дробь, представленная в виде m/n , где НОД(m, n) = 1, имеет конечную десятичную запись тогда и только тогда, когда ее знаменатель . Тогда достаточно сократить числитель и знаменатель на общие множители, а далее выполнить проверку знаменателя.
При x = 68;
Как проверял:
var
x, a, b, i: integer;
begin
for i := 1 to 1000 do
begin
x := i;
a := 0;
b := 0;
while x > 0 do
begin
a := a + 1;
if b < (x mod 8)
then b := x mod 8;
x := x div 8;
end;
if (a = 3) and (b = 4) Then
begin
writeln(i);
break;
end;
end;
end.
Взял 1000 потому что думал, что должно быть меньше. Если бы программа не сработала взял бы либо отрицательные числа, либо больше тысячи (возможно бы пришлось изменить тип данных).
Привожу 2 варианта решения.
Вариант 1: файл 1.cpp
Решение основано на обыкновенном вычислении периода дроби (для дробей, имеющих конечную десятичную запись(например, 1/2=0,5), период вычисляется для формы с нулем в периоде(то есть для 1/2 берется форма 0,5(0))) с деления столбиком.
Замечание: сам алгоритм деления в столбик я писал достаточно давно, и для других программ, поэтому его реализация в данном коде может быть неоптимальной (в плане памяти или кол-ва операций), однако он работает.
Вариант 2: файл 3.cpp
Если немного углубиться в математику, можно найти теорему, по которой дробь, представленная в виде m/n , где НОД(m, n) = 1, имеет конечную десятичную запись тогда и только тогда, когда ее знаменатель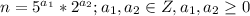
. Тогда достаточно сократить числитель и знаменатель на общие множители, а далее выполнить проверку знаменателя.