Не совсем понимаю, как здесь использовать двоичную матрицу, поэтому решу по-своему.
Шестикласснику не повезло — он не нашёл ни одного гриба, а Петя с пятиклассником нашли много грибов.
Вывод 1: Петя или 7-классник, или 8-классник.
Ваня и семиклассник нашли куст малины и позвали Кирилла полакомиться ягодами.
Вывод 2: Ваня и Кирилл не семиклассники.
Восьмиклассник, шестиклассник и Кирилл объясняли Саше, как ориентироваться на местности.
Вывод 3: Кирилл и Саша или в 5 классе, или в 7 классе.
Вывод 4: Так как 5 и 7 класс - это Кирилл и Саша, пока неизвестно в каком порядке, значит, что Петя не может быть 7-классником. Следовательно, он 8-классник.
Вывод 5: Исходя из вывода 2 и 4, Ваня и Кирилл занимают 5 и 6 класс.
Объединим выводы 3 и 5 - Кирилл в 5 классе, Саша в 7 классе, Ваня в 6 классе.
ответ: 5 класс - Кирилл, 6 класс - Ваня, 7 класс - Саша, 8 класс - Петя.
Решение основано на обыкновенном вычислении периода дроби (для дробей, имеющих конечную десятичную запись(например, 1/2=0,5), период вычисляется для формы с нулем в периоде(то есть для 1/2 берется форма 0,5(0))) с деления столбиком.
Замечание: сам алгоритм деления в столбик я писал достаточно давно, и для других программ, поэтому его реализация в данном коде может быть неоптимальной (в плане памяти или кол-ва операций), однако он работает.
Вариант 2: файл 3.cpp
Если немного углубиться в математику, можно найти теорему, по которой дробь, представленная в виде m/n , где НОД(m, n) = 1, имеет конечную десятичную запись тогда и только тогда, когда ее знаменатель . Тогда достаточно сократить числитель и знаменатель на общие множители, а далее выполнить проверку знаменателя.
Не совсем понимаю, как здесь использовать двоичную матрицу, поэтому решу по-своему.
Шестикласснику не повезло — он не нашёл ни одного гриба, а Петя с пятиклассником нашли много грибов.
Вывод 1: Петя или 7-классник, или 8-классник.
Ваня и семиклассник нашли куст малины и позвали Кирилла полакомиться ягодами.
Вывод 2: Ваня и Кирилл не семиклассники.
Восьмиклассник, шестиклассник и Кирилл объясняли Саше, как ориентироваться на местности.
Вывод 3: Кирилл и Саша или в 5 классе, или в 7 классе.
Вывод 4: Так как 5 и 7 класс - это Кирилл и Саша, пока неизвестно в каком порядке, значит, что Петя не может быть 7-классником. Следовательно, он 8-классник.
Вывод 5: Исходя из вывода 2 и 4, Ваня и Кирилл занимают 5 и 6 класс.
Объединим выводы 3 и 5 - Кирилл в 5 классе, Саша в 7 классе, Ваня в 6 классе.
ответ: 5 класс - Кирилл, 6 класс - Ваня, 7 класс - Саша, 8 класс - Петя.
Привожу 2 варианта решения.
Вариант 1: файл 1.cpp
Решение основано на обыкновенном вычислении периода дроби (для дробей, имеющих конечную десятичную запись(например, 1/2=0,5), период вычисляется для формы с нулем в периоде(то есть для 1/2 берется форма 0,5(0))) с деления столбиком.
Замечание: сам алгоритм деления в столбик я писал достаточно давно, и для других программ, поэтому его реализация в данном коде может быть неоптимальной (в плане памяти или кол-ва операций), однако он работает.
Вариант 2: файл 3.cpp
Если немного углубиться в математику, можно найти теорему, по которой дробь, представленная в виде m/n , где НОД(m, n) = 1, имеет конечную десятичную запись тогда и только тогда, когда ее знаменатель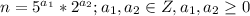
. Тогда достаточно сократить числитель и знаменатель на общие множители, а далее выполнить проверку знаменателя.