Mikrasoft worddasturini oynasining umumiy korinishi

# Задание 1

sumOfElements = 0

numberOfElements = 0

currentNumber = int(input())

while currentNumber != 0:

   sumOfElements += currentNumber

   numberOfElements += 1

   currentNumber = int(input())

if sumOfElements != 0:

   res = sumOfElements / numberOfElements

   res = round(res, 1)

print(res)

# Задание 2

arr = []  # array for divisors

number = int(input())

for i in range(1, number):

   if number % i == 0:

       arr.append(i)

print(sum(arr))

детский вариант:

# Задание 1

res = 0

summ = 0

n = 0

a = int(input())

while a != 0:

   summ = summ + a

   n = n + 1

   a = int(input())

if summ != 0:

   res = summ / n

   res = round(res, 1)

print(res)

# Задача 2

summ = 0

n = int(input())

for i in range(1, n):

   if n % i == 0:

       summ = summ + i

print(summ)

(см. объяснение)

Объяснение:

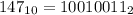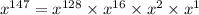Решая задачу "в лоб", нам потребовалось бы умножить число само на себя ровно 147 раз. Это много, потому попробуем оптимизировать алгоритм. Заметим, что , а . Изначально имеем число . Пусть 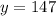- степень. Пусть 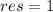- наш будущий ответ. На каждой итерации цикла будем умножать сам на себя, а 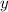целочисленно делить на 2. При этом заметим, что когда 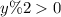, то нам надо умножить текущий результат на . Таким образом, всего за 8 итераций (вместо 147!) мы можем возвести некоторое число в степень 147.

Покажем, как написать это на C++:

#define ll long long

ll bpow(ll x, ll y) {

   ll r = 1;

   while (y > 0) {

       if (y % 2 > 0) {

           r *= x;

       }

       x *= x;

       y /= 2;

   }

   return r;

}

Задание выполнено!