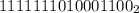представления целого числа со знаком называется "дополнительный код".
Алгоритм представления положительного числа:
1. Перевести число в двоичную систему счисления
2. Записать число в прямом коде в 16-ти двоичных разрядах
1.
2. (дополняем незначащими нулями до 15-ти разрядов и в старшем разряде ставим 0 в качестве знака положительного числа)
Представление числа:
Алгоритм представления отрицательного числа:
1. Перевести модуль числа в двоичную систему счисления
2. Записать число в прямом коде в 16-ти двоичных разрядах
3. Найти обратный код (то есть инвертировать прямой код)
4. Найти дополнительный код, прибавив единицу к обратному коду
1.
2. (обычно дополняют незначащими нулями до 15-ти разрядов и в старшем разряде ставят 1 в качестве знака "-", но также допускается не выставлять значение 1 в знаковом разряде, а на следующем шаге проинвертировать все его разряды, не обращая внимания, знаковый ли это разряд или информационный. Я выбрал второй вариант)
3. (заменяем в прямом коде нули на единицы и наоборот)
Объяснение:
A
class Parrot:
def __init__(self):
self.phrase = 'Привет, друзья!'
def say(self):
print(self.phrase)
p = Parrot()
p.say()
B
class Parrot:
def __init__(self, phrase):
self.phrase = phrase
def say(self):
print(self.phrase)
p1 = Parrot( "Гав!" )
p2 = Parrot( "Мяу!" )
p1.say()
p2.say()
С
class Parrot:
def __init__(self, phrase):
self.phrase = phrase
def say(self):
print(self.phrase)
def newText(self, phrase):
self.phrase = phrase
p = Parrot( "Гав!" )
p.say()
p.newText( "Мяу!" )
p.say()
D
class Parrot:
def __init__(self, phrase):
self.phrase = phrase
def say(self, count=1):
print(self.phrase*count)
def newText(self, phrase):
self.phrase = phrase
p = Parrot( "Гав!" )
p.say()
p.newText( "Мяу!" )
p.say( 3 )
представления целого числа со знаком называется "дополнительный код".
Алгоритм представления положительного числа:
1. Перевести число в двоичную систему счисления
2. Записать число в прямом коде в 16-ти двоичных разрядах
1.
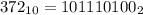
2.
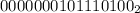(дополняем незначащими нулями до 15-ти разрядов и в старшем разряде ставим 0 в качестве знака положительного числа)
Представление числа: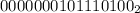
Алгоритм представления отрицательного числа:
1. Перевести модуль числа в двоичную систему счисления
2. Записать число в прямом коде в 16-ти двоичных разрядах
3. Найти обратный код (то есть инвертировать прямой код)
4. Найти дополнительный код, прибавив единицу к обратному коду
1.
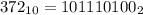
2.
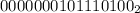(обычно дополняют незначащими нулями до 15-ти разрядов и в старшем разряде ставят 1 в качестве знака "-", но также допускается не выставлять значение 1 в знаковом разряде, а на следующем шаге проинвертировать все его разряды, не обращая внимания, знаковый ли это разряд или информационный. Я выбрал второй вариант)
3.
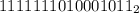(заменяем в прямом коде нули на единицы и наоборот)
4.
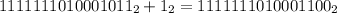
Представление числа: