Мы знаем координаты двух точек, лежащих на прямой. Обозначим их как и . Тогда:
Решение
Мы знаем координаты точек многоугольника.
Для каждого ребра (пары соседних точек) мы должны проверить, чтобы все остальные точки находились по одну сторону от прямой, которой принадлежит эта пара точек.
Т.е., мы перебираем каждое ребро и смотрим, чтобы остальные точки были одного знака.
Оказывается, смотреть все точки необязательно! Нам нужно проверить каждое ребро, чтобы сказать ответ. Поэтому, нам достаточно смотреть лишь положение двух соседних с этим ребром точек относительно ребра.
Итого, мы должны для каждого ребра убедиться, что две соседних с этим ребром точки лежат по одну сторону от ребра. Вот и всё.
Код
#include <bits/stdc++.h>
using namespace std;
int main() {
int n;
cin >> n;
long double x[n+2];
long double y[n+2];
for (int i = 0; i < n; i++) {
cin >> x[i] >> y[i];
}
x[n] = x[0];
y[n] = y[0];
x[n+1] = x[1];
y[n+1] = y[1];
for (int i = 1; i < n; i++) {
long double a = y[i+1] - y[i];
long double b = x[i] - x[i+1];
long double c = y[i] * x[i+1] - x[i]*y[i+1];
if ((a*x[i-1]+b*y[i-1]+c)*(a*x[i+2]+b*y[i+2]+c) < 0) {
...А если интересует решение на классическом Паскале, предлагаю просто поддерживать текущее, предыдущее и пред-предыдущее значения в ряду, и в цикле обновлять ответ.
Обрати внимание! longint может хранить значения только до , поэтому конкретно в этой программе вывод будет достоверным только для N ≤ 46. Ты можешь сделать текущую, предыдущую и пред-предыдущую переменные типа int64, и тогда максимальное значение N возрастёт до 92. Для бОльших N тебе придётся писать длинное сложение.
Общее уравнение прямой: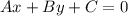
Мы знаем координаты двух точек, лежащих на прямой. Обозначим их как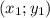
и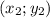 
. Тогда:
Решение
Мы знаем координаты точек многоугольника.
Для каждого ребра (пары соседних точек) мы должны проверить, чтобы все остальные точки находились по одну сторону от прямой, которой принадлежит эта пара точек.
Т.е., мы перебираем каждое ребро и смотрим, чтобы остальные точки были одного знака.
Оказывается, смотреть все точки необязательно! Нам нужно проверить каждое ребро, чтобы сказать ответ. Поэтому, нам достаточно смотреть лишь положение двух соседних с этим ребром точек относительно ребра.
Итого, мы должны для каждого ребра убедиться, что две соседних с этим ребром точки лежат по одну сторону от ребра. Вот и всё.
Код
#include <bits/stdc++.h>
using namespace std;
int main() {
int n;
cin >> n;
long double x[n+2];
long double y[n+2];
for (int i = 0; i < n; i++) {
cin >> x[i] >> y[i];
}
x[n] = x[0];
y[n] = y[0];
x[n+1] = x[1];
y[n+1] = y[1];
for (int i = 1; i < n; i++) {
long double a = y[i+1] - y[i];
long double b = x[i] - x[i+1];
long double c = y[i] * x[i+1] - x[i]*y[i+1];
if ((a*x[i-1]+b*y[i-1]+c)*(a*x[i+2]+b*y[i+2]+c) < 0) {
cout << "NO" << endl;
return 0;
}
}
cout << "YES" << endl;
return 0;
}
...А если интересует решение на классическом Паскале, предлагаю просто поддерживать текущее, предыдущее и пред-предыдущее значения в ряду, и в цикле обновлять ответ.
Обрати внимание! longint может хранить значения только до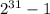
, поэтому конкретно в этой программе вывод будет достоверным только для N ≤ 46. Ты можешь сделать текущую, предыдущую и пред-предыдущую переменные типа int64, и тогда максимальное значение N возрастёт до 92. Для бОльших N тебе придётся писать длинное сложение.
Код
var
i, n, pred, predpred, cur: longint;
begin
read(n);
if n = 1 then writeln(1)
else if n = 2 then writeln('1 1')
else write('1 1 ');
if n < 3 then exit;
pred := 1;
predpred := 1;
for i := 3 to n do
begin
cur := pred + predpred;
write(cur, ' ');
predpred := pred;
pred := cur;
end;
writeln;
end.