Синформатикой - ! 1.какие числа можно записать в натуральной естественной форме , а какие нет: -02.3 05*10 .005 17,02 1/10 2.записать числа в полулогарифмической форме (с использованием символа ге): 4520 0,27 -03400 30*10 -3*100 3.какие числа записаны верно в полулогарифмической форме,какие нет 57e2.4 -5e+25 0.02e1 87,10e3 3e-2 4.расставить порядок действий под выражениям: x*a^5+7*(sqr(2^a)^a/2+x*y)/y/3
запишем условие: по условию даны мощности двух алфавитов
Nm=32, Np=64 количество символов в письмах Km=80, Kp=70
Нужно сравнить информационные объемы писем двух племен Im, Ip
решение: для нахождения информационного объема текста нам нужен вес 1 символа в каждом алфавите. Найдем его:
Nm=2^im, подставим сюда известную величину - 32=2^im
32 - это двойка в четвертой степени, поэтому im=4бит
Np=2^ip, подставим сюда известную величину - 64=2^ip
64 - это двойка в пятой степени, поэтому ip=5бит
Вычислим Im=Km*im=80*4=320 бит, Ip=Kp*ip=70*5=350 бит,
сравним объемы Ip>Im
Итак, целевой язык - С++.
Так как мы с тобой - парни попсовые, то будем делать по красоте. Я хочу получить инструментарий для описания произвольных фигур подобного рода с минимальными изменениями в коде. При этом хочу, чтобы описания этих фигур в коде были наглядными и позволяли представить, как строятся эти фигуры.
В связи с этим, обычное простое математическое описание нам не подходит. Так как банальное разбиение по четвертям и написание вложенных if - путь презрения. Не будь таким.
Что я предлагаю сделать вместо этого? Всё гениальное просто!
Описание предметной области и подхода к решениюПредлагаю воспользоваться свойством расстояний. Как думаешь, какое расстояние имеет точка M(x, y) до окружности O с центром в (0; 0) и радиусом 20? Правильно,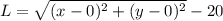
. При чем, если мы возьмем точку, например, М(15, 15), то получим L > 0. Если же возьмём M(3; 3), то получим L <= 0.
Таким образом, используя функции расстояния можно определить, находимся мы внутри объекта или снаружи.
Функции расстояния зависят от вида объекта. Для окружности я привел выше. Для квадрата тоже есть своя функция расстояния.
В нашей задаче мы имеем две окружности Big(0, 0, 20) и Small(0, 0, 10).
При этом из меньшей окружности вырезали первую и третью четверти, что можно выразить как сумму двух квадратов вырезанных из этой окружности: Quarter1(0,0, 10,10) и Quarter3(0,0, -10,-10).
Разность Small и этих двух квадратов даёт нам фигуру вырезанной области, которую мы вычитаем из Big.
Арифметика фигур
Как же работает это сложение? Ну, если мы складываем две фигуры, то нам интересно минимальное расстояние до любой из них. Мы считаем, все их одной фигурой.
Если мы пересекаем две фигуры, то нас интересует максимальное расстояние до любой из них.
Если мы отрицаем фигуру, мы получаем инверсию области. Для большого круга это было бы всё, что вне круга.
Если мы вычитаем фигуры, то нас интересует максимальное расстояние: до первой фигуры или до инверсии вычитаемой фигуры.
Big - (Small - (Quarter1 + Quarter3))
Хотелось бы в коде получить подобное понятное и наглядное описание, как мы привели здесь.
Что мы имеем из этих требований. Набор объектов и методов работы с ними, которые разняться от типа к типу. Как под копирку описание Объектно-ориентированного подхода.
Какие сущности мы можем выделить их описаний?
ТочкаФигураОкружностьПрямоугольник (общий случай квадрата)Фигура-суммаФигура-разностьФигура-пересечениеТочкаПо сути просто набор из координат X и У.
Но есть ряд полезных методов, которые могут нам пригодиться:
Сложение точек;Вычитание точек;Максимальная комбинация;Длина соответствующего вектора.Эти методы сильно упростят нам, простым смертным жизнь.
ФигураОбщее определение для всех других фигур.
Сама по себе ничего не значит: мы ведь не можем знать, круг это или квадрат, или, может, какая комбинация?
Для чего оно надо? Оно даёт обобщение понятия фигура. Есть же у фигур что-то общее, из-за чего их зовут фигурами! В нашем случае:
Для всех фигур можно точно сказать, находится ли точка M внутри;До всех фигур можно посчитать расстояние из точки M;Все фигуры можно складывать, вычитать и пересекать.КругОбъект с точкой О и радиусом R.
Как считать расстояние уже было показано: разница точек -> длина соответствующего вектора - R.
ПрямоугольникЗадаётся 2 точками (A и B), лежащими на одной диагонали прямоугольника.
Расстояние, может показаться, считается хитро, но на самом деле, нет.
В коде можно посмотреть.
Фигура-сложение (объеднинеие)UnitedFigure
Состоит из двух фигур.
Расстояние - минимальное расстояние до одной из фигур.
Фигура-вычитание (дополнение)ComplementedFigure
Состоит из двух фигур.
Расстояние - максимальное расстояние либо до первой фигуры, либо до инверсии второй фигуры.
Фигура-пересечение (пересечение)IntersectedFigure
Состоит из двух фигур.
Расстояние - максимальное расстояние до любой из фигур.
КодПришло время кода! Ура!!
Он простой и с пояснениями. И найти его ты можешь в приложениях к ответу (файл .CPP).
Пример работы приведен на изображении.
Можешь удалить вызовы функций test_this_point.