Рассмотрим i от 7 до 9 - все это числа попадают под условие блока else (потому что не будет выполняться условие i >= 10, а там стоит оператор and, то есть для выполнения условия необходимо две истины)
Таким образом, сначала вывод будет таким:
14 16 18
То есть 7 • 2, 8 • 2, 9 • 2.
Далее рассмотрим числа от 10 до 14. Сразу понимаем, что эти числа попадут в блок if, в котором проверяется четность числа и то, больше ли оно 10. Все эти числа больше 10. Выбираем чётные: 10, 12, 14.
45 / 16 = 13 и 2 в остатке, 13 в шестнадцатеричной системе D
Значит
*Для перевода двоичного числа в десятичное необходимо его записать в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа 2, и вычислить по правилам десятичной арифметики.
*Для перевода десятичного числа в шестнадцатеричную систему его необходимо последовательно делить на 16 до тех пор, пока не останется остаток, меньший или равный 15. Число в шестнадцатеричной системе записывается как последовательность цифр последнего результата деления и остатков от деления в обратном порядке.
14 16 18 5 6 7
Объяснение:
Рассмотрим i от 7 до 9 - все это числа попадают под условие блока else (потому что не будет выполняться условие i >= 10, а там стоит оператор and, то есть для выполнения условия необходимо две истины)
Таким образом, сначала вывод будет таким:
14 16 18
То есть 7 • 2, 8 • 2, 9 • 2.
Далее рассмотрим числа от 10 до 14. Сразу понимаем, что эти числа попадут в блок if, в котором проверяется четность числа и то, больше ли оно 10. Все эти числа больше 10. Выбираем чётные: 10, 12, 14.
Таким образом, конечный вывод будет таким:
14 16 18 5 6 7
ответ:
Объяснение:
45 / 16 = 13 и 2 в остатке, 13 в шестнадцатеричной системе D
Значит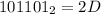
*Для перевода двоичного числа в десятичное необходимо его записать в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа 2, и вычислить по правилам десятичной арифметики.
*Для перевода десятичного числа в шестнадцатеричную систему его необходимо последовательно делить на 16 до тех пор, пока не останется остаток, меньший или равный 15. Число в шестнадцатеричной системе записывается как последовательность цифр последнего результата деления и остатков от деления в обратном порядке.