1.найдите все натуральные значения n для которых оба числа 9n+ 28 и n + 5 есть точными квадратами
2.на доске записано 10 единиц и 10 двоек. за один ход разрешается стирать любые две цифры и если они будут одинаковыми записать двойку а если разными единицу. если последняя цифра остающихся на доске единица то выигрывает первый игрок если же двойка то другой. у кого из игроков выигрышная стратегия
3.в треугольнике abc проведены биссектрисы bd. известно, что центр описанной вокруг треугольника abc окружности совпадает с центром окружности что вписано в bdc .знайдить углы abc
ответ: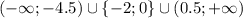
Пошаговое объяснение:
Если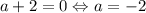
Уравнение имеет два решения, значит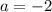 подходит
подходит
Если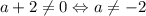 , то в совокупности два квадратных уравнения
, то в совокупности два квадратных уравнения
Тогда, либо их корни должны совпадать, что произойдет в случае, когда совпадают уравнения, т.е. при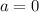 , убедимся, что корни есть
, убедимся, что корни есть 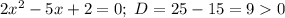
Либо одно из них имеет единственный корень, который совпадает с одним из двух корней другого, что невозможно, поскольку у этих уравнений совпадает сумма корней (по т. Виета она равна 5/(a+2))
Также подходят все значения параметра, при котором одно из них имеет 2 корня, а другое не имеет решений
Поскольку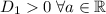 , то оно всегда имеет 2 корня, найдем при каких значениях параметра уравнение (2) не имеет корней
, то оно всегда имеет 2 корня, найдем при каких значениях параметра уравнение (2) не имеет корней
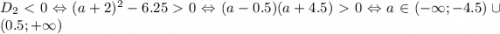
Итого получим, что уравнение имеет два решения при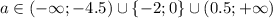
1)
3х-3<х-3 5х+15>2х+3
2х<0 3х>-12
х<0 х>-4
Потом чертишь числовую прямую на которой отмечаешь точку 0 и -4
ответ:х принадлежит (-4;0)
2)
{ 2(y-2) >= 3y+1
{ 5(y+1) <= 4y+3
Раскрываем скобки
{ 2y - 4 >= 3y + 1
{ 5y + 5 <= 4y + 3
Упрощаем
{ y <= -5
{ y <= -2
ответ: y = (-oo; -5]
3)
{ 3(2y-3) <= y+6
{ 4(3y+1) >= 5y-10
Раскрываем скобки
{ 6y - 9 <= y + 6
{ 12y + 4 >= 5y - 10
Упрощаем
{ 5y <= 15; y <= 3
{ 7y >= -14; y >= -2
ответ: y = [-2; 3]
4)
{ 2(3x+2) > 5(x-1)
{ 7(x+2) < 3(2x+3)
Раскрываем скобки
{ 6x + 4 > 5x - 5
{ 7x + 14 < 6x + 9
Упрощаем
{ x > -9
{ x < -5
ответ: x = (-9; -5)